学习方式是看高翔的视觉SLAM十四讲
学习视频:https://www.bilibili.com/video/BV16t411g7FR
学习参考代码:https://github.com/gaoxiang12/slambook
学习实现代码:https://github.com/bonbon-rj/learn_slam
单目:移动相机产生深度
双目:通过两个摄像头视差产生深度
深度相机(RGBD):通过物理方法得到深度(受光照影响大)
1.前端(VO)
2.后端(Optimization)
3.回环检测(Loop Closing)
4.建图(Mapping)
向量内积,结果是个值,表示两个向量的相似程度,结果与点积一致
⟨ a , b ⟩ = ∣ a ∣ ∣ b ∣ c o s θ = ∑ i = 1 3 a i b i = a ⋅ b = a T b \langle a, b \rangle = \vert a\vert \vert b \vert cos\theta =\sum_{i=1}^{3}a_ib_i= a \cdot b = a^T b
⟨ a , b ⟩ = ∣ a ∣ ∣ b ∣ c o s θ = i = 1 ∑ 3 a i b i = a ⋅ b = a T b
向量外积,结果是个向量,符合右手螺旋定则,结果与叉乘一致
a ⊗ b = a × b = [ a 2 b 3 − a 3 b 2 , a 3 b 1 − a 1 b 3 , a 1 b 2 − a 2 b 1 ] T = [ 0 − a 3 a 2 a 3 0 − a 1 − a 2 a 1 0 ] [ b 1 b 2 b 3 ] a \otimes b =
a \times b =
[a_2b_3-a_3b_2,a_3b_1-a_1b_3,a_1b_2-a_2b_1]^T=
\begin{bmatrix}
0 & -a_3 & a_2 \\
a_3 & 0 & -a_1 \\
-a_2 & a_1 & 0
\end{bmatrix}
\begin{bmatrix}
b_1 \\
b_2 \\
b_3
\end{bmatrix}
a ⊗ b = a × b = [ a 2 b 3 − a 3 b 2 , a 3 b 1 − a 1 b 3 , a 1 b 2 − a 2 b 1 ] T = ⎣ ⎢ ⎡ 0 a 3 − a 2 − a 3 0 a 1 a 2 − a 1 0 ⎦ ⎥ ⎤ ⎣ ⎢ ⎡ b 1 b 2 b 3 ⎦ ⎥ ⎤
特殊正交群:S O ( 3 ) = { R ∈ R 3 × 3 ∣ R R T = I , d e t ( R ) = 1 } SO(3)=\{R \in R^{3 \times 3}|RR^T=I,det(R)=1 \} S O ( 3 ) = { R ∈ R 3 × 3 ∣ R R T = I , d e t ( R ) = 1 }
特殊欧式群:S E ( 3 ) = { T = [ R t 0 1 ] , R ∈ S O ( 3 ) , t ∈ R 3 } SE(3)=\{T=\begin{bmatrix}R&t\\0&1 \end{bmatrix},R\in SO(3),t \in R^3\} S E ( 3 ) = { T = [ R 0 t 1 ] , R ∈ S O ( 3 ) , t ∈ R 3 }
齐次变换矩阵求逆:T − 1 = [ R T − R T t 0 1 ] T^{-1}=\begin{bmatrix} R^T &-R^Tt \\ 0 & 1\end{bmatrix} T − 1 = [ R T 0 − R T t 1 ]
一般将T W T_W T W T R T_R T R T R W T_{RW} T R W T W R T_{WR} T W R
向量a a a n n n θ \theta θ b b b
则w = θ n w=\theta n w = θ n n n n
角轴转化为旋转矩阵:R = c o s θ I + ( 1 − c o s θ ) n n T + s i n θ n ^ R=cos\theta I+(1-cos\theta)nn^T+sin\theta \hat n R = c o s θ I + ( 1 − c o s θ ) n n T + s i n θ n ^
旋转矩阵到轴角:θ = a r c c o s t r ( R ) − 1 2 \theta = arccos\frac{tr(R)-1}{2} θ = a r c c o s 2 t r ( R ) − 1 R n = n Rn=n R n = n A x = λ x Ax=\lambda x A x = λ x n n n R R R
绕着自身坐标系旋转
Z轴:偏航,X轴:翻滚,Y轴:俯仰
存在万向锁问题:
比如在ZYX欧拉角中,若pitch为正负90°时,第一次和第三次旋转是绕同一个轴,丢失一个自由度
在复变函数中,复数乘以i i i
进一步地,单位圆上的复数可以表示二维平面的旋转
四元数q = q 0 + q 1 i + q 2 j + q 3 k q=q_0+q_1i+q_2j+q_3k q = q 0 + q 1 i + q 2 j + q 3 k
四元数常表示成一个实部和虚部向量 q = [ s , v ] , s = q 0 ∈ R , v = [ q 1 , q 2 , q 3 ] T ∈ R 3 q=[s,v],s=q_0 \in R,v=[q_1,q_2,q_3]^T \in R^3 q = [ s , v ] , s = q 0 ∈ R , v = [ q 1 , q 2 , q 3 ] T ∈ R 3
虚部之间的关系,i 2 = j 2 = k 2 = − 1 i^2=j^2=k^2=-1 i 2 = j 2 = k 2 = − 1 i j = k , j k = i , k i = j ij=k,jk=i,ki=j i j = k , j k = i , k i = j
可以将i j k ijk i j k x y z xyz x y z
假设q a = [ s a , v a ] = s a + x a i + y a j + z a k q_a = [s_a,v_a]=s_a+x_ai+y_aj+z_ak q a = [ s a , v a ] = s a + x a i + y a j + z a k q b = [ s b , v b ] = s b + x b i + y b j + z b k q_b=[s_b,v_b]=s_b+x_bi+y_bj+z_bk q b = [ s b , v b ] = s b + x b i + y b j + z b k
加减:q a ± q b = [ s a ± s b , v a ± v b ] q_a \pm q_b=[s_a \pm s_b,v_a \pm v_b] q a ± q b = [ s a ± s b , v a ± v b ]
乘法:q a q b = [ s a s b − v a T v b , s a v b + s b v a + v a × v b ] q_aq_b=[s_as_b-v_a^Tv_b,s_av_b+s_bv_a+v_a \times v_b] q a q b = [ s a s b − v a T v b , s a v b + s b v a + v a × v b ]
共轭:q a ∗ = [ s a , − v a ] q_a^*=[s_a,-v_a] q a ∗ = [ s a , − v a ]
模长(范数):∣ ∣ q a ∣ ∣ = s a 2 + x a 2 + y a 2 + z a 2 \vert \vert q_a\vert \vert=\sqrt{s_a^2+x_a^2+y_a^2+z_a^2} ∣ ∣ q a ∣ ∣ = s a 2 + x a 2 + y a 2 + z a 2
逆:q − 1 = q ∗ ∣ ∣ q ∣ ∣ 2 q^{-1}=\frac{q^*}{\vert \vert q\vert \vert^2} q − 1 = ∣ ∣ q ∣ ∣ 2 q ∗
数乘:k q a = [ k s a , k v a ] kq_a=[ks_a,kv_a] k q a = [ k s a , k v a ]
点乘:q a ⋅ q b = s a s b + x a x b i + y a y b j + z a z b k q_a \cdot q_b=s_as_b+x_ax_bi+y_ay_bj+z_az_bk q a ⋅ q b = s a s b + x a x b i + y a y b j + z a z b k
角轴到四元数:q = [ c o s θ 2 , n x s i n θ 2 , n y s i n θ 2 , n z s i n θ 2 ] T q=[cos\frac{\theta}{2},n_xsin\frac{\theta}{2},n_ysin\frac{\theta}{2},n_zsin\frac{\theta}{2}]^T q = [ c o s 2 θ , n x s i n 2 θ , n y s i n 2 θ , n z s i n 2 θ ] T
四元数到角轴:θ = 2 a r c c o s q 0 , [ n x , n y , n z ] T = [ q 1 , q 2 , q 3 ] T s i n θ 2 \theta=2arccosq_0,[n_x,n_y,n_z]^T=\frac{[q_1,q_2,q_3]^T}{sin\frac{\theta}{2}} θ = 2 a r c c o s q 0 , [ n x , n y , n z ] T = s i n 2 θ [ q 1 , q 2 , q 3 ] T
假设p 0 = ( x , y , z ) p_0=(x,y,z) p 0 = ( x , y , z ) p = [ 0 , x , y , z ] = [ 0 , v ] p=[0,x,y,z]=[0,v] p = [ 0 , x , y , z ] = [ 0 , v ]
则经过四元数q q q p ′ = q p q − 1 p' = qpq^{-1} p ′ = q p q − 1
四元数相比于角轴、欧拉角的优点:紧凑、无奇异性
绕x轴旋转α \alpha α R o t ( x ⃗ , α ) = [ 1 0 0 0 C α − S α 0 S α C α ] Rot(\vec{x},\alpha)=\begin{bmatrix} 1 & 0 & 0 \\ 0 & C\alpha & -S\alpha \\ 0 & S\alpha & C\alpha\end{bmatrix} R o t ( x , α ) = ⎣ ⎢ ⎡ 1 0 0 0 C α S α 0 − S α C α ⎦ ⎥ ⎤
绕y轴旋转β \beta β R o t ( y ⃗ , β ) = [ C β 0 S β 0 1 0 − S β 0 C β ] Rot(\vec{y},\beta)=\begin{bmatrix} C\beta & 0 & S\beta \\ 0 & 1 & 0 \\ -S\beta & 0 & C\beta\end{bmatrix} R o t ( y , β ) = ⎣ ⎢ ⎡ C β 0 − S β 0 1 0 S β 0 C β ⎦ ⎥ ⎤
绕z轴旋转γ \gamma γ R o t ( z ⃗ , γ ) = [ C γ − S γ 0 S γ C γ 0 0 0 1 ] Rot(\vec{z},\gamma)=\begin{bmatrix} C\gamma & -S\gamma & 0 \\ S\gamma & C\gamma & 0 \\ 0 & 0 & 1\end{bmatrix} R o t ( z , γ ) = ⎣ ⎢ ⎡ C γ S γ 0 − S γ C γ 0 0 0 1 ⎦ ⎥ ⎤
sudo apt-get install libeigen3-dev # 安装
whereis eigen3 # 查看库位置 显示/usr/include/eigen3
locate eigen3 | grep include # 模糊搜索 表示含有eigen3的所有包含include的路径
表示刚体在三维的运动后,我们还要对其进行估计和优化
角轴是旋转矩阵对应的李代数,相对于旋转矩阵,优化时无约束
且引出李代数是为了进行求导等操作
群是一种集合加上一种运算的代数结构
记集合为A A A ⋅ \cdot ⋅ ( A , ⋅ ) (A ,\cdot) ( A , ⋅ )
1.封闭性:∀ a 1 , a 2 ∈ A , a 1 ⋅ a 2 ∈ A \forall a_1,a_2 \in A,a_1 \cdot a_2 \in A ∀ a 1 , a 2 ∈ A , a 1 ⋅ a 2 ∈ A
2.结合律:∀ a 1 , a 2 , a 3 ∈ A , ( a 1 ⋅ a 2 ) ⋅ a 3 = a 1 ⋅ ( a 2 ⋅ a 3 ) \forall a_1,a_2,a_3 \in A,(a_1 \cdot a_2) \cdot a_3=a_1 \cdot (a_2 \cdot a_3) ∀ a 1 , a 2 , a 3 ∈ A , ( a 1 ⋅ a 2 ) ⋅ a 3 = a 1 ⋅ ( a 2 ⋅ a 3 )
3.幺元:∃ a 0 ∈ A , ∀ a ∈ A , a 0 ⋅ a = a ⋅ a 0 = a \exists a_0 \in A, \forall a \in A,a_0 \cdot a = a \cdot a_0 = a ∃ a 0 ∈ A , ∀ a ∈ A , a 0 ⋅ a = a ⋅ a 0 = a a 0 a_0 a 0
辅助理解就是 运算为加时a 0 a_0 a 0 a 0 a_0 a 0
4.逆:∀ a ∈ A , ∃ a − 1 ∈ A , a ⋅ a − 1 = a 0 \forall a \in A,\exists a^{-1} \in A, a \cdot a^{-1} = a_0 ∀ a ∈ A , ∃ a − 1 ∈ A , a ⋅ a − 1 = a 0
G L ( n ) GL(n) G L ( n ) n × n n \times n n × n
S O ( n ) SO(n) S O ( n )
S E ( n ) SE(n) S E ( n )
设G G G G G G G G G
1.具有连续(光滑)性质的群
2.既是群也是流形
3.一个刚体在空间中能连续地运动
S O ( 3 ) SO(3) S O ( 3 ) S E ( 3 ) SE(3) S E ( 3 )
李代数由一个集合V V V F F F [ , ] [,] [ , ]
如果满足以下性质,则称( V , F , [ , ] ) (V,F,[,]) ( V , F , [ , ] ) g g g
1.封闭性 2.双线性 3.自反性 4.雅克比等价
其中二元运算[ , ] [,] [ , ]
在李代数s o ( 3 ) = { ϕ ∈ R 3 , ϕ ^ ∈ R 3 × 3 } so(3)=\{ {\phi \in R^3,\hat \phi \in R^{3 \times 3} } \} s o ( 3 ) = { ϕ ∈ R 3 , ϕ ^ ∈ R 3 × 3 }
李括号为[ ϕ 1 , ϕ 2 ] = ( ϕ ^ 1 ϕ ^ 2 − ϕ ^ 2 ϕ ^ 1 ) ˇ [\phi_1,\phi_2]=(\hat \phi_1 \hat \phi_2 - \hat \phi_2 \hat \phi_1)\check{} [ ϕ 1 , ϕ 2 ] = ( ϕ ^ 1 ϕ ^ 2 − ϕ ^ 2 ϕ ^ 1 ) ˇ
其中 ^ \hat{} ^ ˇ \check{} ˇ
假设三维向量a = [ a 1 a 2 a 3 ] a = \begin{bmatrix} a_1\\a_2\\a_3 \end{bmatrix} a = ⎣ ⎢ ⎡ a 1 a 2 a 3 ⎦ ⎥ ⎤ a ^ = A = [ 0 − a 3 a 2 a 3 0 − a 1 − a 2 a 1 0 ] \hat a = A = \begin{bmatrix} 0&-a_3&a_2\\a_3& 0&-a_1\\-a_2 & a_1 & 0 \end{bmatrix} a ^ = A = ⎣ ⎢ ⎡ 0 a 3 − a 2 − a 3 0 a 1 a 2 − a 1 0 ⎦ ⎥ ⎤
A A A a a a
在李代数s e ( 3 ) = { ξ = [ p ϕ ] ∈ R 6 , ρ ∈ R 3 , ϕ ∈ s o ( 3 ) , ξ ^ = [ ϕ ^ ρ 0 T 0 ] ∈ R 4 × 4 } se(3)=\{ \xi = \begin{bmatrix} p \\ \phi\end{bmatrix} \in R^6,\rho \in R^3,\phi \in so(3), \hat \xi = \begin{bmatrix} \hat \phi &\rho \\ 0^T & 0\end{bmatrix} \in R^{4 \times 4}\} s e ( 3 ) = { ξ = [ p ϕ ] ∈ R 6 , ρ ∈ R 3 , ϕ ∈ s o ( 3 ) , ξ ^ = [ ϕ ^ 0 T ρ 0 ] ∈ R 4 × 4 }
李括号为[ ξ 1 , ξ 2 ] = ( ξ ^ 1 ξ ^ 2 − ξ ^ 2 ξ ^ 1 ) ˇ [\xi_1,\xi_2]=(\hat \xi_1 \hat \xi_2 -\hat \xi_2 \hat \xi_1)\check {} [ ξ 1 , ξ 2 ] = ( ξ ^ 1 ξ ^ 2 − ξ ^ 2 ξ ^ 1 ) ˇ
其中 ^ \hat{} ^ ˇ \check{} ˇ
假设六维向量a = [ ρ 1 ρ 2 ρ 3 ϕ 1 ϕ 2 ϕ 3 ] = [ ρ ϕ ] a =\begin{bmatrix} \rho_1 \\ \rho_2 \\ \rho_3 \\ \phi_1 \\ \phi_2 \\ \phi_3\end{bmatrix}=\begin{bmatrix} \rho \\ \phi\end{bmatrix} a = ⎣ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎡ ρ 1 ρ 2 ρ 3 ϕ 1 ϕ 2 ϕ 3 ⎦ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎤ = [ ρ ϕ ] a ^ = [ 0 − ϕ 3 ϕ 2 ρ 1 ϕ 3 0 − ϕ 1 ρ 2 − ϕ 2 ϕ 1 0 ρ 3 0 0 0 0 ] \hat a=\begin{bmatrix} 0&-\phi_3&\phi_2 &\rho_1\\\phi_3& 0&-\phi_1&\rho_2\\-\phi_2 & \phi_1 & 0 &\rho_3 \\ 0&0&0&0\end{bmatrix} a ^ = ⎣ ⎢ ⎢ ⎢ ⎡ 0 ϕ 3 − ϕ 2 0 − ϕ 3 0 ϕ 1 0 ϕ 2 − ϕ 1 0 0 ρ 1 ρ 2 ρ 3 0 ⎦ ⎥ ⎥ ⎥ ⎤
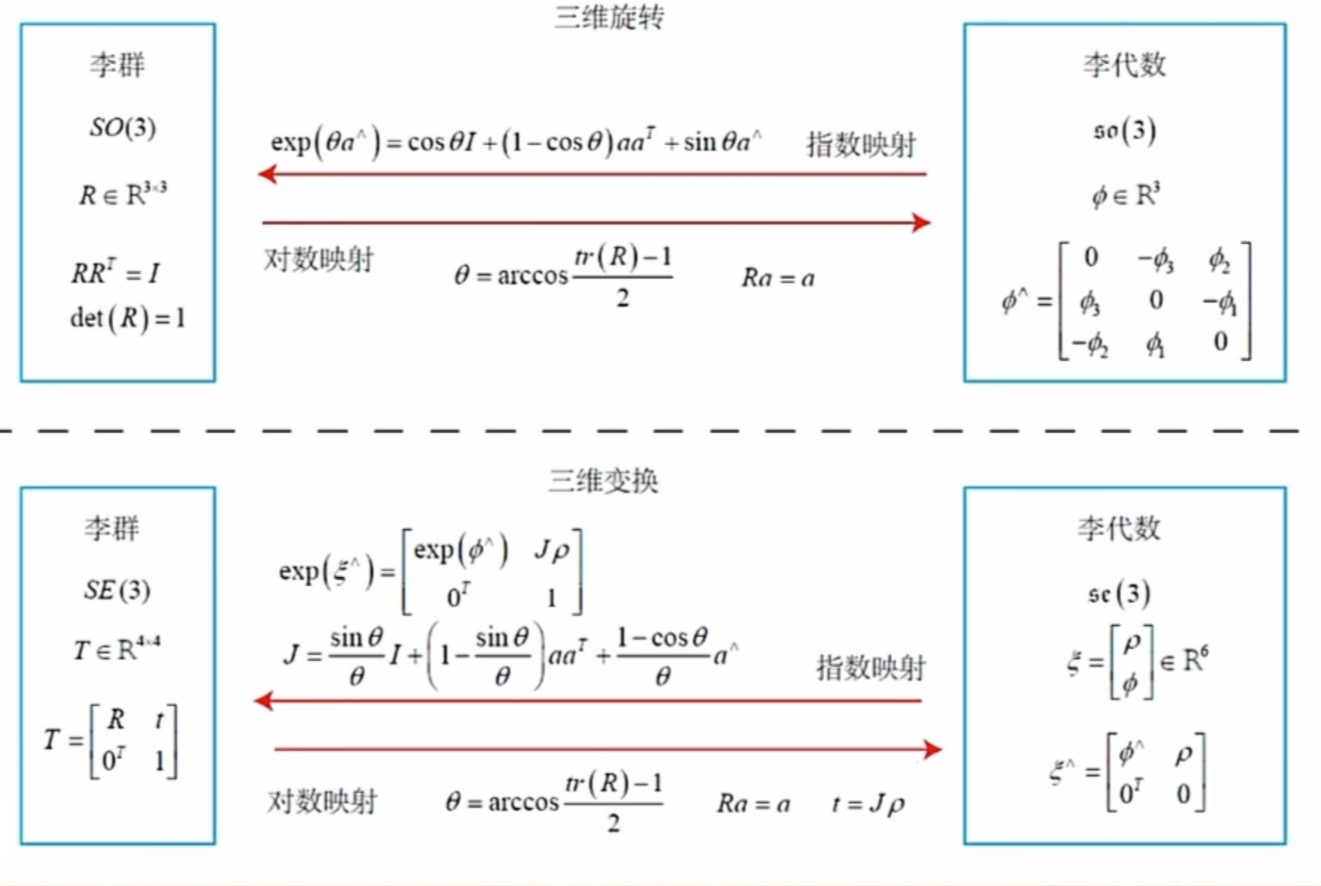
每个李代数都有与之对应的李群,位于向量空间,实际是李群单位元处的正切空间
S O ( 3 ) SO(3) S O ( 3 ) s o ( 3 ) so(3) s o ( 3 ) S E ( 3 ) SE(3) S E ( 3 ) s e ( 3 ) se(3) s e ( 3 )
李代数可以通过指数映射转换为李群,李群也可以通过对数映射转换为李代数
李群与李代数的指数映射关系是通过正交性且连续然后求导化简而得
指数映射关系化简是使用了泰勒展开加一些反对称矩阵高次规律进行化简而得
例如对于S O ( 3 ) SO(3) S O ( 3 ) R = e x p ( θ a ^ ) = c o s θ I + ( 1 − c o s θ ) a a T + s i n θ a ^ R = exp(\theta \hat a)=cos\theta I+(1-cos\theta)aa^T+sin\theta \hat a R = e x p ( θ a ^ ) = c o s θ I + ( 1 − c o s θ ) a a T + s i n θ a ^ s o ( 3 ) so(3) s o ( 3 )
具体S O ( 3 ) SO(3) S O ( 3 ) s o ( 3 ) so(3) s o ( 3 ) S E ( 3 ) SE(3) S E ( 3 ) s e ( 3 ) se(3) s e ( 3 )
我再自己梳理一遍:
S O ( 3 ) SO(3) S O ( 3 ) 3 × 3 3 \times 3 3 × 3 R R R s o ( 3 ) so(3) s o ( 3 ) 3 × 1 3 \times 1 3 × 1 ϕ = θ n = [ ϕ 1 ϕ 2 ϕ 3 ] \phi=\theta n=\begin{bmatrix} \phi_1 \\ \phi_2 \\ \phi_3\end{bmatrix} ϕ = θ n = ⎣ ⎢ ⎡ ϕ 1 ϕ 2 ϕ 3 ⎦ ⎥ ⎤
S O ( 3 ) SO(3) S O ( 3 ) s o ( 3 ) so(3) s o ( 3 ) θ = a r c c o s t r ( R ) − 1 2 \theta = arccos \frac{tr(R)-1}{2} θ = a r c c o s 2 t r ( R ) − 1 R n = n Rn=n R n = n
s o ( 3 ) so(3) s o ( 3 ) S O ( 3 ) SO(3) S O ( 3 ) R = c o s θ I + ( 1 − c o s θ ) n n T + s i n θ n ^ R=cos\theta I+(1-cos\theta)nn^T+sin\theta \hat n R = c o s θ I + ( 1 − c o s θ ) n n T + s i n θ n ^
S E ( 3 ) SE(3) S E ( 3 ) 4 × 4 4 \times 4 4 × 4 T = [ R t 0 1 ] T=\begin{bmatrix} R &t \\ 0 & 1\end{bmatrix} T = [ R 0 t 1 ] s e ( 3 ) se(3) s e ( 3 ) 6 × 1 6 \times 1 6 × 1 ξ = [ ρ 1 ρ 2 ρ 3 ϕ 1 ϕ 2 ϕ 3 ] = [ ρ n θ ] = [ ρ ϕ ] \xi =\begin{bmatrix} \rho_1 \\ \rho_2 \\ \rho_3 \\ \phi_1 \\ \phi_2 \\ \phi_3\end{bmatrix}=\begin{bmatrix} \rho \\ n\theta\end{bmatrix}=\begin{bmatrix} \rho \\ \phi\end{bmatrix} ξ = ⎣ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎡ ρ 1 ρ 2 ρ 3 ϕ 1 ϕ 2 ϕ 3 ⎦ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎤ = [ ρ n θ ] = [ ρ ϕ ]
其中有雅克比J = s i n θ θ I + ( 1 − s i n θ θ ) n n T + 1 − c o s θ θ n ^ J=\frac{sin\theta}{\theta}I+(1-\frac{sin\theta}{\theta})nn^T+\frac{1-cos\theta}{\theta}\hat n J = θ s i n θ I + ( 1 − θ s i n θ ) n n T + θ 1 − c o s θ n ^
S E ( 3 ) SE(3) S E ( 3 ) s e ( 3 ) se(3) s e ( 3 ) θ = a r c c o s t r ( R ) − 1 2 \theta = arccos \frac{tr(R)-1}{2} θ = a r c c o s 2 t r ( R ) − 1 R n = n Rn=n R n = n t = J ρ t = J\rho t = J ρ
s e ( 3 ) se(3) s e ( 3 ) S E ( 3 ) SE(3) S E ( 3 ) T = [ c o s θ I + ( 1 − c o s θ ) n n T + s i n θ n ^ J ρ 0 1 ] T =\begin{bmatrix} cos\theta I+(1-cos\theta)nn^T+sin\theta \hat n &J\rho \\ 0 & 1\end{bmatrix} T = [ c o s θ I + ( 1 − c o s θ ) n n T + s i n θ n ^ 0 J ρ 1 ]
对于三维向量a = [ a 1 a 2 a 3 ] a=\begin{bmatrix} a_1\\a_2\\a_3 \end{bmatrix} a = ⎣ ⎢ ⎡ a 1 a 2 a 3 ⎦ ⎥ ⎤ a ^ = [ 0 − a 3 a 2 a 3 0 − a 1 − a 2 a 1 0 ] \hat a = \begin{bmatrix} 0&-a_3&a_2\\a_3& 0&-a_1\\-a_2 & a_1 & 0 \end{bmatrix} a ^ = ⎣ ⎢ ⎡ 0 a 3 − a 2 − a 3 0 a 1 a 2 − a 1 0 ⎦ ⎥ ⎤
对于六维向量a = [ a 1 a 2 a 3 b 1 b 2 b 3 ] = [ a b ] a=\begin{bmatrix} a_1\\a_2\\a_3\\b_1\\b_2\\b_3 \end{bmatrix}=\begin{bmatrix} a\\b \end{bmatrix} a = ⎣ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎡ a 1 a 2 a 3 b 1 b 2 b 3 ⎦ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎤ = [ a b ] a ^ = [ b ^ a 0 0 ] \hat a=\begin{bmatrix} \hat b &a \\ 0 & 0\end{bmatrix} a ^ = [ b ^ 0 a 0 ] a , b a,b a , b a a a
从李群到李代数,是为了可以求导等操作,因为在李群上做加法不封闭
一般情况下,在李代数中做加法与李群上做乘法不等价,由BCH公式可证:
e x p ( ϕ ^ 1 ) e x p ( ϕ ^ 2 ) ≠ e x p ( ( ϕ 1 + ϕ 2 ) ^ ) exp(\hat \phi_1)exp(\hat \phi_2) \neq exp((\phi_1+\phi_2)\hat{})
e x p ( ϕ ^ 1 ) e x p ( ϕ ^ 2 ) = e x p ( ( ϕ 1 + ϕ 2 ) ^ )
特别地,当其中有一个小量时,可以近似获得:(加粗括号是取下三角部分)
( l n ( e x p ( ϕ ^ 1 ) e x p ( ϕ ^ 2 ) ) ) ˇ ≈ { J l ( ϕ 2 ) − 1 ϕ 1 + ϕ 2 , i f ϕ 1 i s s m a l l J r ( ϕ 1 ) − 1 ϕ 2 + ϕ 1 , i f ϕ 2 i s s m a l l (ln(exp(\hat \phi_1)exp(\hat \phi_2)))\check {} \approx \left\{\begin{matrix} J_l(\phi_2)^{-1}\phi_1+\phi_2 ,if \, \, \phi_1 \, \, is \,\,small \\ J_r(\phi_1)^{-1}\phi_2+\phi_1 ,if \, \, \phi_2 \, \, is \,\,small \end{matrix}\right.
( l n ( e x p ( ϕ ^ 1 ) e x p ( ϕ ^ 2 ) ) ) ˇ ≈ { J l ( ϕ 2 ) − 1 ϕ 1 + ϕ 2 , i f ϕ 1 i s s m a l l J r ( ϕ 1 ) − 1 ϕ 2 + ϕ 1 , i f ϕ 2 i s s m a l l
其中J l J_l J l J r J_r J r
J l = s i n θ θ I + ( 1 − s i n θ θ ) n n T + 1 − c o s θ θ n ^ J_l = \frac{sin\theta}{\theta}I+(1-\frac{sin\theta}{\theta})nn^T+\frac{1-cos\theta}{\theta}\hat n
J l = θ s i n θ I + ( 1 − θ s i n θ ) n n T + θ 1 − c o s θ n ^
J r ( ϕ ) = J l ( − ϕ ) J_r(\phi)=J_l(-\phi)
J r ( ϕ ) = J l ( − ϕ )
左乘雅克比的逆为:
J l − 1 = θ 2 c o t θ 2 I + ( 1 − θ 2 c o t θ 2 ) n n T − θ 2 n ^ J_l^{-1} = \frac{\theta}{2}cot\frac{\theta}{2}I+(1-\frac{\theta}{2}cot\frac{\theta}{2})nn^T-\frac{\theta}{2}\hat n
J l − 1 = 2 θ c o t 2 θ I + ( 1 − 2 θ c o t 2 θ ) n n T − 2 θ n ^
在S O ( 3 ) SO(3) S O ( 3 ) s o ( 3 ) so(3) s o ( 3 )
李群左乘小量,有:
e x p ( ( Δ ϕ ) ^ ) e x p ( ϕ ^ ) = e x p ( ( ϕ + J l − 1 ( ϕ ) Δ ϕ ) ^ ) , exp((\Delta \phi)\hat{})exp( \phi \hat{})=exp({(}\phi+J_l^{-1}(\phi)\Delta\phi)\hat{}),
e x p ( ( Δ ϕ ) ^ ) e x p ( ϕ ^ ) = e x p ( ( ϕ + J l − 1 ( ϕ ) Δ ϕ ) ^ ) ,
李代数加小量,有:
e x p ( ( ϕ + Δ ϕ ) ^ ) = e x p ( ( J l Δ ϕ ) ^ ) e x p ( ϕ ^ ) = e x p ( ϕ ^ ) e x p ( ( J r Δ ϕ ) ^ ) exp((\phi+\Delta\phi )\hat {}) =exp((J_l \Delta\phi)\hat{})exp( \phi\hat{})=exp( \phi\hat{})exp((J_r \Delta\phi)\hat{})
e x p ( ( ϕ + Δ ϕ ) ^ ) = e x p ( ( J l Δ ϕ ) ^ ) e x p ( ϕ ^ ) = e x p ( ϕ ^ ) e x p ( ( J r Δ ϕ ) ^ )
有了上述前提,我们可以求解李代数上的导数
如果点p p p R R R p ′ p' p ′ p ′ p' p ′ R R R
可以考虑对R R R ϕ \phi ϕ Δ \Delta Δ p ′ p' p ′ Δ \Delta Δ
可以考虑对R R R Δ \Delta Δ p ′ p' p ′ Δ \Delta Δ
对于S 0 ( 3 ) S0(3) S 0 ( 3 ) δ \delta δ p p p R R R J l J_l J l
导数模型:∂ ( e x p ( ϕ ^ ) p ) ∂ δ = − ( R p ) ^ J l \frac{\partial( exp(\hat \phi)p)}{\partial \delta}=-(Rp)\hat{}J_l ∂ δ ∂ ( e x p ( ϕ ^ ) p ) = − ( R p ) ^ J l
扰动模型:∂ R p ∂ δ = − ( R p ) ^ \frac{\partial Rp}{\partial \delta}=-(Rp)\hat{} ∂ δ ∂ R p = − ( R p ) ^
对于S E ( 3 ) SE(3) S E ( 3 ) ξ \xi ξ p p p T = [ R t 0 1 ] T=\begin{bmatrix} R & t \\ 0 &1\end{bmatrix} T = [ R 0 t 1 ]
扰动模型:∂ ( T p ) ∂ ξ = [ I − ( R p + t ) ^ 0 T 0 T ] \frac{\partial (Tp)}{\partial \xi} =\begin{bmatrix} I & -(Rp+t) \hat{} \\ 0^T & 0 ^T \end{bmatrix} ∂ ξ ∂ ( T p ) = [ I 0 T − ( R p + t ) ^ 0 T ]
git clone https://github.com/strasdat/Sophus.git
cd Sophus
mkdir build
cd build
cmake ..
make
sudo make install # 实现效果为 把头文件放在了include目录下,把库文件放在了lib目录下
可能是Sophus版本不同,我的使用与视频中不一致
需要在CMakeLists中需要添加一句才不会报错
target_link_libraries (${PROJECT_NAME} Sophus::Sophus)
然后代码编写也是很多不相同,不一一列举。
观测方程由相机观测模型组成
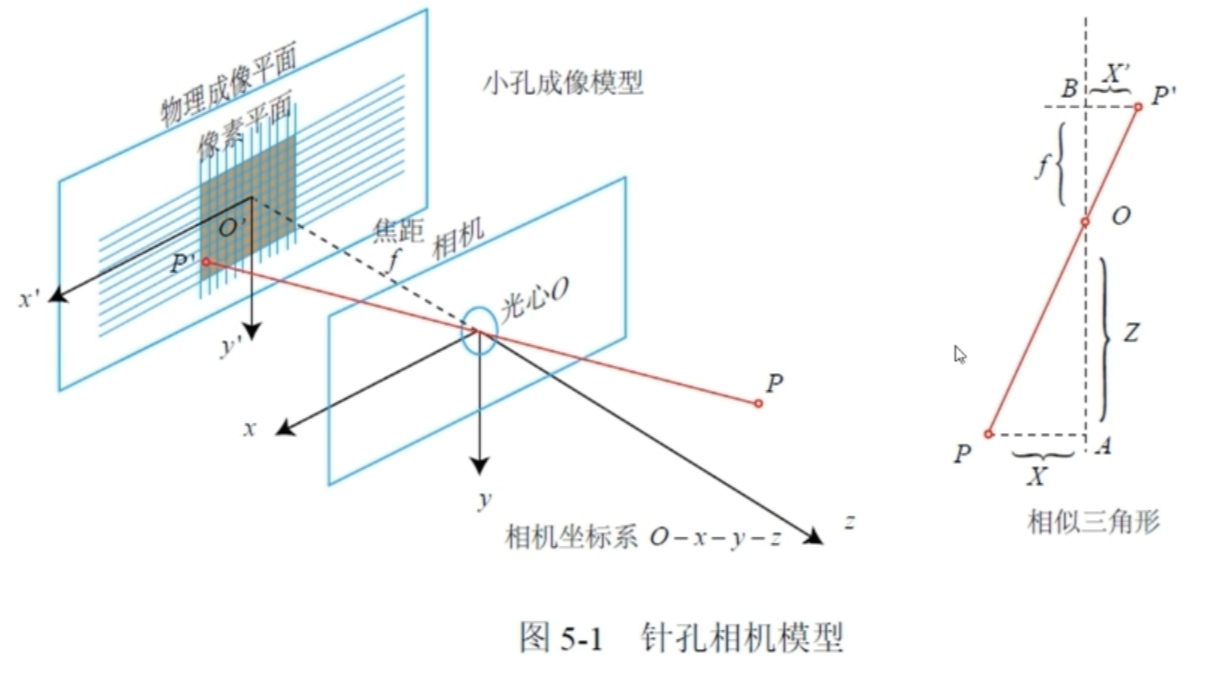
假设一点相对于光心的坐标为( X , Y , Z ) (X,Y,Z) ( X , Y , Z ) ( X ′ , Y ′ ) (X',Y') ( X ′ , Y ′ ) m m m
小孔成像原理,并将图像翻转到前面(倒像转正像),可得
X ′ = f X Z X' = f \frac{X}{Z}
X ′ = f Z X
Y ′ = f Y Z Y' = f\frac{Y}{Z}
Y ′ = f Z Y
假设像素平面像素坐标为( u , v ) (u,v) ( u , v )
u = α X ′ + c x u=\alpha X'+c_x
u = α X ′ + c x
v = β Y ′ + c y v=\beta Y'+c_y
v = β Y ′ + c y
α , β \alpha,\beta α , β m m m
c x , c y c_x,c_y c x , c y
联立可得
u = α f X Z + c x = f x X Z + c x u = \alpha f \frac{X}{Z}+c_x = f_x \frac{X}{Z}+c_x
u = α f Z X + c x = f x Z X + c x
v = β f Y Z + c y = f y Y Z + c y v = \beta f \frac{Y}{Z}+c_y = f_y \frac{Y}{Z}+c_y
v = β f Z Y + c y = f y Z Y + c y
写成矩阵为
Z [ u v 1 ] = [ f x 0 c x 0 f y c y 0 0 1 ] [ X Y Z ] = K P Z\begin{bmatrix} u \\ v \\ 1\end{bmatrix} =\begin{bmatrix} f_x & 0 & c_x \\ 0 &f_y&c_y \\0&0& 1\end{bmatrix}\begin{bmatrix} X \\ Y \\ Z\end{bmatrix} = KP
Z ⎣ ⎢ ⎡ u v 1 ⎦ ⎥ ⎤ = ⎣ ⎢ ⎡ f x 0 0 0 f y 0 c x c y 1 ⎦ ⎥ ⎤ ⎣ ⎢ ⎡ X Y Z ⎦ ⎥ ⎤ = K P
其中K K K
但是要注意,如果缩放图像,内参是改变了
一般我们已知的是世界坐标系下的一点的坐标P w P_w P w
这一点在世界坐标系和相机坐标系之间存在变换P = R P w + t P=RP_w+t P = R P w + t
这里的R , t R,t R , t
由于镜头透镜等原因等,图形成像存在畸变(广角、鱼眼)
假设像素离光心的距离为r r r θ \theta θ
真实坐标为( x t , y t ) (x_t,y_t) ( x t , y t ) ( x , y ) (x,y) ( x , y )
径向畸变(与r r r
x t = x ( 1 + k 1 r 2 + k 2 r 4 + k 3 r 6 ) x_t =x(1+k_1r^2+k_2r^4+k_3r^6)
x t = x ( 1 + k 1 r 2 + k 2 r 4 + k 3 r 6 )
y t = y ( 1 + k 1 r 2 + k 2 r 4 + k 3 r 6 ) y_t =y(1+k_1r^2+k_2r^4+k_3r^6)
y t = y ( 1 + k 1 r 2 + k 2 r 4 + k 3 r 6 )
切向畸变(与θ \theta θ
x t = x + 2 p 1 x y + p 2 ( r 2 + 2 x 2 ) x_t = x+2p_1xy+p_2(r^2+2x^2)
x t = x + 2 p 1 x y + p 2 ( r 2 + 2 x 2 )
y t = y + 2 p 2 x y + p 1 ( r 2 + 2 y 2 ) y_t = y+2p_2xy+p_1(r^2+2y^2)
y t = y + 2 p 2 x y + p 1 ( r 2 + 2 y 2 )
整合结果为:
x t = x ( 1 + k 1 r 2 + k 2 r 4 + k 3 r 6 ) + 2 p 1 x y + p 2 ( r 2 + 2 x 2 ) x_t =x(1+k_1r^2+k_2r^4+k_3r^6)+2p_1xy+p_2(r^2+2x^2)
x t = x ( 1 + k 1 r 2 + k 2 r 4 + k 3 r 6 ) + 2 p 1 x y + p 2 ( r 2 + 2 x 2 )
y t = y ( 1 + k 1 r 2 + k 2 r 4 + k 3 r 6 ) + 2 p 2 x y + p 1 ( r 2 + 2 y 2 ) y_t =y(1+k_1r^2+k_2r^4+k_3r^6)+2p_2xy+p_1(r^2+2y^2)
y t = y ( 1 + k 1 r 2 + k 2 r 4 + k 3 r 6 ) + 2 p 2 x y + p 1 ( r 2 + 2 y 2 )
畸变参数在标定中获得
1.已知世界坐标系下一点P w P_w P w
2.通过R , t R,t R , t P = R P w + t P=RP_w+t P = R P w + t
3.将P P P Z = 1 Z=1 Z = 1 P c = 1 Z P P_c = \frac{1}{Z}P P c = Z 1 P
4.将P c P_c P c P c t P_{ct} P c t
5.将P c t P_{ct} P c t K K K ( u , v ) (u,v) ( u , v ) [ u v 1 ] = K P c t \begin{bmatrix} u \\ v \\ 1\end{bmatrix} = KP_{ct} ⎣ ⎢ ⎡ u v 1 ⎦ ⎥ ⎤ = K P c t
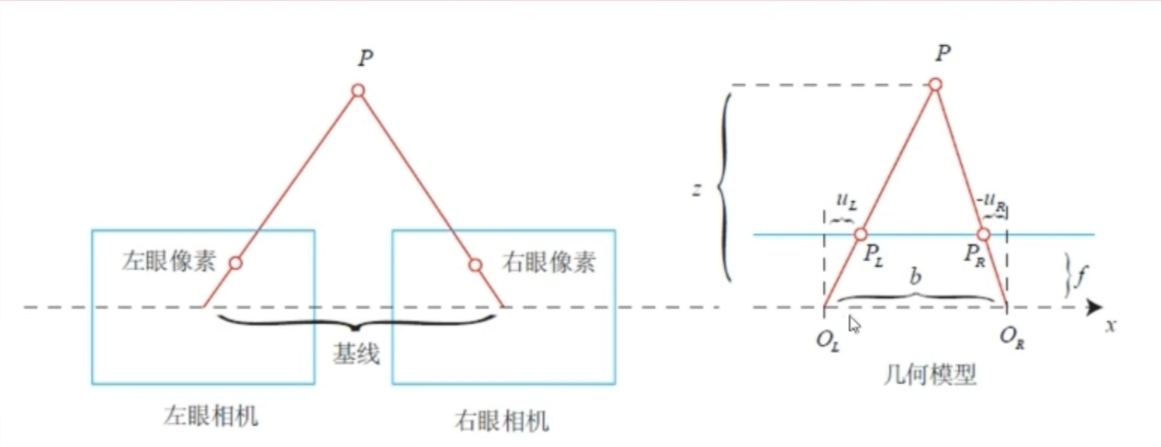
假设两个相机共面平行摆放,
假设空间中一点在左相机的坐标为( u l , v l ) (u_l,v_l) ( u l , v l ) ( u r , v r ) (u_r,v_r) ( u r , v r )
两相机光心距离(基线)b b b f f f
则有:
z − f z = b − u l + u r b \frac{z-f}{z}=\frac{b-u_l+u_r}{b}
z z − f = b b − u l + u r
整理可得z = f b u l − u r z=\frac{fb}{u_l-u_r} z = u l − u r f b
其中u l − u r u_l-u_r u l − u r d d d
视差最小为一个像素,所以双目可测的最大距离为f b fb f b
物理手段获得图像深度,主要有结构光和TOF两种原理,受光以及被测物体材质影响
opencv和pcl我都安装过了,所以没有安装过程
注意一下pcl的实现中,CMakeLists中编译要用C++17,不然编译可能报错(或者奇奇怪怪的bug)
参考:http://eigen.tuxfamily.org/dox-devel/group__TopicUnalignedArrayAssert.html
pcl点云图最终效果
pcl_viewer map.pcd
运动方程:x k = f ( x k − 1 , u k , w k ) x_k=f(x_{k-1},u_k,w_k) x k = f ( x k − 1 , u k , w k )
x k x_k x k
u k u_k u k
w k w_k w k
运动方程是描述当前与之前位置的关系
观测方程:z k , j = h ( y j , x k , v k , j ) z_{k,j}=h(y_j,x_k,v_{k,j}) z k , j = h ( y j , x k , v k , j )
y j y_j y j
x k x_k x k
v k , j v_{k,j} v k , j
z k , j z_{k,j} z k , j
观测方程描述世界坐标中一点与摄像头像素点之间的关系,也就是之前的相机模型
SLAM研究定位与建图,也就对应了x k x_k x k y j y_j y j
以往是用滤波器 来求解状态估计,而现在非线性优化 成为主流
状态估计可以描述为条件分布P ( x ∣ z , u ) P(x \vert z,u) P ( x ∣ z , u )
在视觉SLAM中,考虑只有观测z z z P ( x ∣ z ) P(x \vert z) P ( x ∣ z )
由贝叶斯法则可以得:
P ( x ∣ z ) = P ( z ∣ x ) P ( x ) P ( z ) ∝ P ( z ∣ x ) P ( x ) P(x \vert z)=\frac{P(z \vert x)P(x)}{P(z)} \propto P(z \vert x)P(x)
P ( x ∣ z ) = P ( z ) P ( z ∣ x ) P ( x ) ∝ P ( z ∣ x ) P ( x )
P ( x ∣ z ) P(x \vert z) P ( x ∣ z ) P ( z ∣ x ) P(z \vert x) P ( z ∣ x ) P ( x ) P(x) P ( x )
最大后验估计(MAP):求解使得P ( z ∣ x ) P ( x ) P(z\vert x)P(x) P ( z ∣ x ) P ( x ) x x x
最大似然估计(MLE):求解使得P ( z ∣ x ) P(z\vert x) P ( z ∣ x ) x x x
假设某次观测z k , j = h ( y j , x k ) + v k , j z_{k,j}=h(y_j,x_k)+v_{k,j} z k , j = h ( y j , x k ) + v k , j v k , j ∼ N ( 0 , Q k , j ) v_{k,j} \sim N(0,Q_{k,j}) v k , j ∼ N ( 0 , Q k , j ) z k , j z_{k,j} z k , j x k , y j x_k,y_j x k , y j
所以P ( z j , k ∣ x k , y j ) = N ( h ( y j , x k ) , Q k , j ) P(z_{j,k} \vert x_k,y_j)=N(h(y_j,x_k),Q_{k,j}) P ( z j , k ∣ x k , y j ) = N ( h ( y j , x k ) , Q k , j )
这里涉及到知识,假设X ∼ ( μ , σ 2 ) X \sim(\mu,\sigma^2) X ∼ ( μ , σ 2 ) a X + b ∼ ( a μ + b , a 2 σ 2 ) aX+b \sim (a\mu+b,a^2\sigma^2) a X + b ∼ ( a μ + b , a 2 σ 2 )
而对于高斯分布X ∼ ( μ , ∑ ) X \sim(\mu,\sum) X ∼ ( μ , ∑ )
P ( x ) = 1 ( 2 π ) N d e t ( ∑ ) e x p ( − 1 2 ( x − μ ) T ∑ − 1 ( x − μ ) ) P(x)=\frac{1}{\sqrt{({2\pi})^Ndet(\sum)}}exp(-\frac{1}{2}({x-\mu})^T\sum {}^{-1}(x-\mu))
P ( x ) = ( 2 π ) N d e t ( ∑ ) 1 e x p ( − 2 1 ( x − μ ) T ∑ − 1 ( x − μ ) )
取负对数
− l n ( P ( x ) ) = 1 2 l n ( ( 2 π ) N d e t ( ∑ ) ) + 1 2 ( x − μ ) T ∑ − 1 ( x − μ ) -ln(P(x))=\frac{1}{2}ln(({2\pi})^Ndet(\sum))+\frac{1}{2}({x-\mu})^T\sum {}^{-1}(x-\mu)
− l n ( P ( x ) ) = 2 1 l n ( ( 2 π ) N d e t ( ∑ ) ) + 2 1 ( x − μ ) T ∑ − 1 ( x − μ )
求解高斯分布最大化相当于求解负对数最小化
而结果包含两项,前一项与x x x
所以最终相当于求解使得( x − μ ) T ∑ − 1 ( x − μ ) ({x-\mu})^T\sum {}^{-1}(x-\mu) ( x − μ ) T ∑ − 1 ( x − μ ) x x x
即x ∗ = a r g m i n ( ( z k , j − h ( y j , x k ) ) T Q k , j − 1 ( z k , j − h ( y j , x k ) ) ) x^* =argmin(({z_{k,j}-h(y_j,x_k)})^TQ_{k,j}^{-1}(z_{k,j}-h(y_j,x_k))) x ∗ = a r g m i n ( ( z k , j − h ( y j , x k ) ) T Q k , j − 1 ( z k , j − h ( y j , x k ) ) )
而求解式子是个二次型,也被称为最小二乘
二次型复习一下,一般形式:
f ( x 1 , x 2 , ⋅ , x n ) = a 11 x 1 2 + a 22 x 2 2 + ⋅ ⋅ ⋅ + a n n x n 2 + 2 a 12 x 1 x 2 + 2 a 13 x 1 x 3 + ⋅ ⋅ ⋅ + 2 a ( n − 1 ) n x n − 1 x n f(x_1,x_2,\cdot,x_n)=a_{11}x_1^2+a_{22}x_2^2+\cdot \cdot\cdot+a_{nn}x_n^2+2a_{12}x_1x_2+2a_{13}x_1x_3+\cdot \cdot \cdot+2a_{(n-1)n}x_{n-1}x_n
f ( x 1 , x 2 , ⋅ , x n ) = a 1 1 x 1 2 + a 2 2 x 2 2 + ⋅ ⋅ ⋅ + a n n x n 2 + 2 a 1 2 x 1 x 2 + 2 a 1 3 x 1 x 3 + ⋅ ⋅ ⋅ + 2 a ( n − 1 ) n x n − 1 x n
而二次型可以写成矩阵的形式,例如
a x 2 + 2 b x y + c y 2 ax^2+2bxy+cy^2 a x 2 + 2 b x y + c y 2 [ x y ] [ a b b c ] [ x y ] = X T A X \begin{bmatrix} x&y\end{bmatrix}\begin{bmatrix} a&b\\b&c\end{bmatrix}\begin{bmatrix} x\\y\end{bmatrix}=X^TAX [ x y ] [ a b b c ] [ x y ] = X T A X
对于一般化问题
x k = f ( x k − 1 , u k , w k ) x_k=f(x_{k-1},u_k,w_k)
x k = f ( x k − 1 , u k , w k )
z k , j = h ( y j , x k , v k , j ) z_{k,j}=h(y_j,x_k,v_{k,j})
z k , j = h ( y j , x k , v k , j )
定义运动误差和观测误差,也就是当前值减期望值
e v , k = x k − f ( x k − 1 , u k ) e_{v,k}=x_k-f(x_{k-1},u_k)
e v , k = x k − f ( x k − 1 , u k )
e y , j , k = z k , j − h ( x k , y j ) e_{y,j,k}=z_{k,j}-h(x_k,y_j)
e y , j , k = z k , j − h ( x k , y j )
上述栗子只有考虑观测方程,类比上述栗子结果形式,并求和可得最小化函数
J ( x ) = ∑ k e v , k T R k − 1 e v , k + ∑ k ∑ j e y , k , j T Q k , j − 1 e y , k , j J(x)=\sum_ke_{v,k}^TR_k^{-1}e_{v,k}+\sum_k\sum_je_{y,k,j}^TQ_{k,j}^{-1}e_{y,k,j}
J ( x ) = k ∑ e v , k T R k − 1 e v , k + k ∑ j ∑ e y , k , j T Q k , j − 1 e y , k , j
即求解使得J ( x ) J(x) J ( x ) x , y x,y x , y
对于任意函数f ( x ) f(x) f ( x ) x x x 1 2 ∣ ∣ f ( x ) ∣ ∣ 2 2 \frac{1}{2} {\vert \vert f(x) \vert \vert_2}^2 2 1 ∣ ∣ f ( x ) ∣ ∣ 2 2
若d f ( x ) d x = 0 \frac{df(x)}{dx}=0 d x d f ( x ) = 0
一般地,d f ( x ) d x = 0 \frac{df(x)}{dx}=0 d x d f ( x ) = 0
迭代方式:
1.给定初始值x 0 x_0 x 0
2.寻找增量Δ x k \Delta x_k Δ x k 1 2 ∣ ∣ f ( x + Δ x k ) ∣ ∣ 2 2 \frac{1}{2}{\vert \vert f(x+\Delta x_k )\vert \vert_2}^2 2 1 ∣ ∣ f ( x + Δ x k ) ∣ ∣ 2 2
3.满足终止条件(Δ x k \Delta x_k Δ x k
4.不满足终止条件,x k + 1 = x k + Δ x k x_{k+1}=x_k+\Delta x_k x k + 1 = x k + Δ x k
确定Δ x k \Delta x_k Δ x k
∣ ∣ f ( x + Δ x ) ∣ ∣ 2 2 ≈ ∣ ∣ f ( x ) ∣ ∣ 2 2 + J ( x ) Δ x + 1 2 Δ x H Δ x T + ⋅ ⋅ ⋅ {\vert \vert f(x+\Delta x) \vert \vert_2}^2 \approx {\vert \vert f(x) \vert \vert_2}^2+J(x)\Delta x+\frac{1}{2}\Delta xH\Delta x^T+\cdot \cdot \cdot
∣ ∣ f ( x + Δ x ) ∣ ∣ 2 2 ≈ ∣ ∣ f ( x ) ∣ ∣ 2 2 + J ( x ) Δ x + 2 1 Δ x H Δ x T + ⋅ ⋅ ⋅
若取一阶:
Δ x \Delta x Δ x Δ x ∗ = − J T ( x ) \Delta x^*=-J^T(x) Δ x ∗ = − J T ( x )
其中J ( x ) J(x) J ( x )
存在zigzag问题(过于贪婪),迭代次数多
若取二阶:
另目标函数对Δ x \Delta x Δ x H Δ x = − J T ( x ) H \Delta x=-J^T(x) H Δ x = − J T ( x )
其中H H H
需要计算复杂的海塞矩阵
即采用二阶,又不需要计算海塞的方法:
1.Gauss-Newton
一阶近似f ( x ) f(x) f ( x ) f ( x + Δ x ) ≈ f ( x ) + J ( x ) Δ x f(x+\Delta x) \approx f(x)+J(x)\Delta x f ( x + Δ x ) ≈ f ( x ) + J ( x ) Δ x
带入目标函数1 2 ∣ ∣ f ( x + Δ x ) ∣ ∣ 2 2 \frac{1}{2}{\vert \vert f(x+\Delta x )\vert \vert_2}^2 2 1 ∣ ∣ f ( x + Δ x ) ∣ ∣ 2 2 Δ x \Delta x Δ x
J T ( x ) J ( x ) Δ x = − J T ( x ) f ( x ) J^T(x)J(x)\Delta x=-J^T(x)f(x)
J T ( x ) J ( x ) Δ x = − J T ( x ) f ( x )
所以对于迭代时的x k x_k x k J ( x k ) J(x_k) J ( x k ) f ( x k ) f(x_k) f ( x k ) Δ x \Delta x Δ x
但是没有办法保证J T ( x ) J ( x ) J^T(x)J(x) J T ( x ) J ( x )
2.Levenberg-Marquadt
该方法一定程度保证高斯牛顿的方程可解
LM方法属于信赖区域方法,认为近似只在区域内可靠
对于一阶近似:f ( x + Δ x ) ≈ f ( x ) + J ( x ) Δ x f(x+\Delta x) \approx f(x)+J(x)\Delta x f ( x + Δ x ) ≈ f ( x ) + J ( x ) Δ x
定义近似程度描述:ρ = f ( x + Δ x ) − f ( x ) J ( x ) Δ x \rho = \frac{f(x+\Delta x)-f(x)}{J(x)\Delta x} ρ = J ( x ) Δ x f ( x + Δ x ) − f ( x )
若ρ \rho ρ
若ρ \rho ρ
所以相当于在高斯牛顿法基础上,增加了区域约束
min Δ x 1 2 ∣ ∣ f ( x k ) + J ( x k ) Δ x k ∣ ∣ 2 , ∣ ∣ D Δ x k ∣ ∣ 2 ≤ μ \min_{\Delta x} \frac{1}{2} {\vert\vert f(x_k)+J(x_k)\Delta x_k \vert\vert}^2, {\vert\vert D\Delta x_k \vert\vert}^2 \leq \mu
Δ x min 2 1 ∣ ∣ f ( x k ) + J ( x k ) Δ x k ∣ ∣ 2 , ∣ ∣ D Δ x k ∣ ∣ 2 ≤ μ
其中Levenberg令D D D I I I D D D
利用Lagrange乘子转化为无约束,得最小化函数
1 2 ∣ ∣ f ( x k ) + J ( x k ) Δ x k ∣ ∣ 2 + λ 2 ∣ ∣ D Δ x k ∣ ∣ 2 \frac{1}{2} {\vert\vert f(x_k)+J(x_k)\Delta x_k \vert\vert}^2+\frac{\lambda}{2} {\vert\vert D\Delta x_k \vert\vert}^2
2 1 ∣ ∣ f ( x k ) + J ( x k ) Δ x k ∣ ∣ 2 + 2 λ ∣ ∣ D Δ x k ∣ ∣ 2
同样展开化简,令对Δ x \Delta x Δ x
( J T ( x ) J ( x ) + λ D T D ) Δ x = − J T ( x ) f ( x ) (J^T(x)J(x)+\lambda D^TD)\Delta x=-J^T(x)f(x)
( J T ( x ) J ( x ) + λ D T D ) Δ x = − J T ( x ) f ( x )
可以理解为在J T ( x ) J ( x ) J^T(x)J(x) J T ( x ) J ( x )
对于方程的理解,可以看出二阶和一阶的结合,λ \lambda λ
LM求解非线性最小二乘的方法:
对于任意函数f ( x ) f(x) f ( x ) x x x 1 2 ∣ ∣ f ( x ) ∣ ∣ 2 2 \frac{1}{2} {\vert \vert f(x) \vert \vert_2}^2 2 1 ∣ ∣ f ( x ) ∣ ∣ 2 2
1.给定初始值x 0 x_0 x 0 μ \mu μ
2.对于第k k k Δ x k \Delta x_k Δ x k
( J T ( x k ) J ( x k ) + λ D T D ) Δ x k = − J T ( x k ) f ( x k ) (J^T(x_k)J(x_k)+\lambda D^TD)\Delta x_k=-J^T(x_k)f(x_k)
( J T ( x k ) J ( x k ) + λ D T D ) Δ x k = − J T ( x k ) f ( x k )
3.计算ρ = f ( x + Δ x ) − f ( x ) J ( x ) Δ x \rho= \frac{f(x+\Delta x)-f(x)}{J(x)\Delta x} ρ = J ( x ) Δ x f ( x + Δ x ) − f ( x ) μ = { 2 μ , ρ > 3 4 0.5 μ , ρ < 1 4 \mu =\left\{\begin{matrix} 2\mu,&\rho>\frac{3}{4} \\0.5\mu,&\rho<\frac{1}{4}\end{matrix}\right. μ = { 2 μ , 0 . 5 μ , ρ > 4 3 ρ < 4 1
4.若ρ \rho ρ x k + 1 = x k + Δ x k x_{k+1}=x_k+\Delta x_k x k + 1 = x k + Δ x k
5.判断算法是否收敛,不收敛则返回2,收敛则结束
Google Ceres Solver是通用最小二乘问题求解库
安装参考官网教程:http://www.ceres-solver.org/installation.html
# 先参考官网安装依赖
# 安装
git clone https://github.com/ceres-solver/ceres-solver.git
cd ceres-solver/
mkdir ceres-bin
cd ceres-bin
cmake .. # 可能会卡在 Detected Ceres being used as a git submodule
make
make test
sudo make install
# 测试
bin/simple_bundle_adjuster ../data/problem-16-22106-pre.txt
ceres需要借助源码中提供的CeresConfig.cmake.in文件帮忙找到库
该文件在ceres-solver/cmake中
在项目目录下创建一个cmake_modules文件夹,把该文件放在其中
CMakeLists.txt中添加以下字句即可
set (CMAKE_MODULE_PATH ${PROJECT_SOURCE_DIR} /cmake_modules)
但是我使用的时候不需要这一步也可以成功编译
g2o是图优化库,安装参考:https://zhuanlan.zhihu.com/p/363025399
g2o的使用需要注意几个问题
1.CMakeLists.txt中c++版本要14,编译模式是Release,不然编译不通过
2.课程所给代码编译会报错,部分指针需要转换成智能指针unique_ptr
3.g2o需要借助源码中提供的FindG2O.cmake文件帮忙找到库,在g2o/cmake_modules
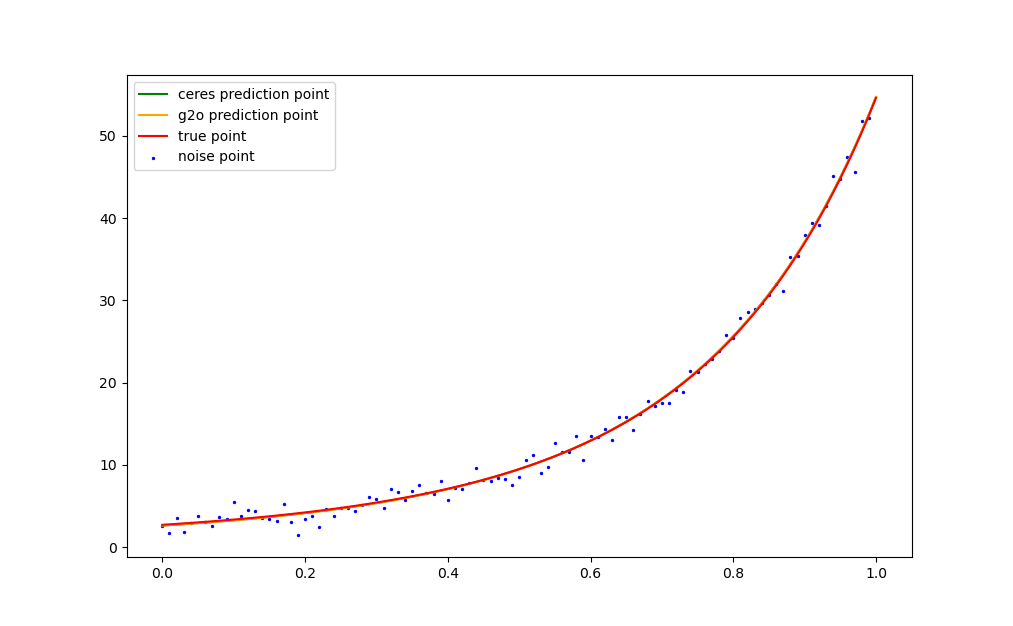
最后用python画图如下
特征点的特点:1.可重复性 2.可区分性 3.提取高效 4.跟图像局部相关
描述子:特征点周围的图像信息,用于区分不同特征点
FAST:一个像素点周围一圈n n n m m m
Oriented FAST:在FAST基础上计算了旋转,特征的旋转是由灰度质心法实现的。
灰度质心法实现如下:
对于图像块B B B m p q = ∑ x , y ∈ B x p y q I ( x , y ) , p , q = { 0 , 1 } m_{pq}=\sum_{x,y \in B}x^py^qI(x,y),\,\,\, p,q=\{0,1\} m p q = ∑ x , y ∈ B x p y q I ( x , y ) , p , q = { 0 , 1 }
通过矩找到图像块的质心:C = ( m 10 m 00 , m 01 m 00 ) C=(\frac{m_{10}}{m_{00}},\frac{m_{01}}{m_{00}}) C = ( m 0 0 m 1 0 , m 0 0 m 0 1 )
质心C C C O O O O C ⃗ \vec{OC} O C θ = a t a n ( m 01 m 10 ) \theta=atan(\frac{m_{01}}{m_{10}}) θ = a t a n ( m 1 0 m 0 1 )
BRIEF是一种二进制描述,在特征点附近的多次像素比较。
以BRIEF-128为例
假设pattern为
{ [ ( Δ x 1 1 , Δ y 1 1 ) , ( Δ x 2 1 , Δ y 2 1 ) ] , [ ( Δ x 1 2 , Δ y 1 2 ) , ( Δ x 2 2 , Δ y 2 2 ) ] , ⋅ ⋅ ⋅ , [ ( Δ x 1 n , Δ y 1 n ) , ( Δ x 2 n , Δ y 2 n ) ] } n = 128 \{ [(\Delta x_{1}^1,\Delta y_{1}^1),(\Delta x_{2}^1,\Delta y_{2}^1)],[(\Delta x_{1}^2,\Delta y_{1}^2),(\Delta x_{2}^2,\Delta y_{2}^2)],\cdot\cdot\cdot,[(\Delta x_{1}^n,\Delta y_{1}^n),(\Delta x_{2}^n,\Delta y_{2}^n)] \}_{n=128}
{ [ ( Δ x 1 1 , Δ y 1 1 ) , ( Δ x 2 1 , Δ y 2 1 ) ] , [ ( Δ x 1 2 , Δ y 1 2 ) , ( Δ x 2 2 , Δ y 2 2 ) ] , ⋅ ⋅ ⋅ , [ ( Δ x 1 n , Δ y 1 n ) , ( Δ x 2 n , Δ y 2 n ) ] } n = 1 2 8
则它的BRIEF由128位组成,每一位为{ 1 I ( x + Δ x 1 n , y + Δ y 1 n ) > I ( x + Δ x 2 n , y + Δ y 2 n ) 0 I ( x + Δ x 1 n , y + Δ y 1 n ) ≤ I ( x + Δ x 2 n , y + Δ y 2 n ) \left\{\begin{matrix} 1 &I(x+\Delta x_{1}^n,y+\Delta y_{1}^n)>I(x+\Delta x_{2}^n,y+\Delta y_{2}^n)\\0&I(x+\Delta x_{1}^n,y+\Delta y_{1}^n)\leq I(x+\Delta x_{2}^n,y+\Delta y_{2}^n)\end{matrix}\right. { 1 0 I ( x + Δ x 1 n , y + Δ y 1 n ) > I ( x + Δ x 2 n , y + Δ y 2 n ) I ( x + Δ x 1 n , y + Δ y 1 n ) ≤ I ( x + Δ x 2 n , y + Δ y 2 n )
ORB中采用旋转之后的BRIEF,比较特征点的描述子,需要用到汉明距离。
通过描述子的差异判断是否为同一点
方法右:暴力匹配,快速最近邻(FLANN)等
特征匹配后,只有两个单目图像中特征点之间的对应关系,可以求解两相机之间的旋转和平移,2D-2D
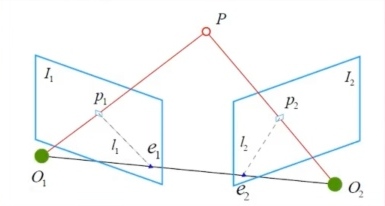
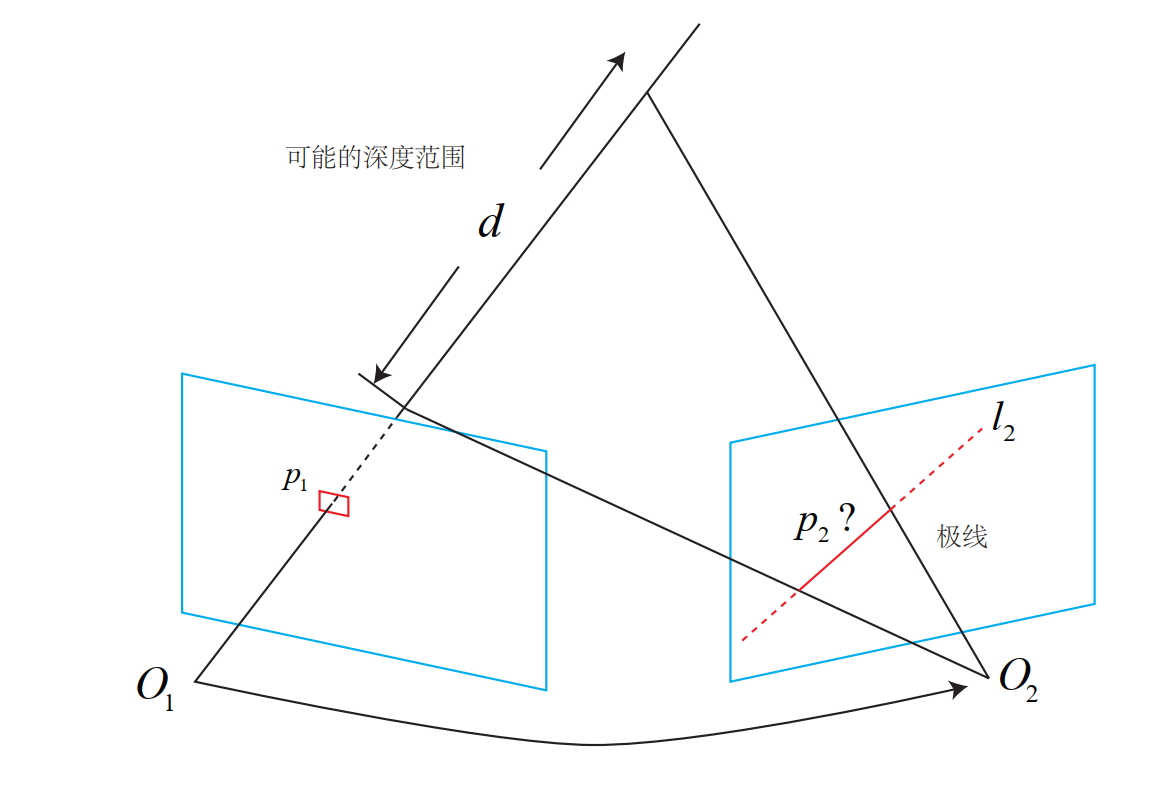
下图反应的是同一个点在两个图像之间的对应关系
其中p p p p 1 , p 2 p_1,p_2 p 1 , p 2 I 1 I_1 I 1 I 2 I_2 I 2
O 1 , O 2 O_1,O_2 O 1 , O 2 I 1 I_1 I 1 I 2 I_2 I 2 e 1 , e 2 e_1,e_2 e 1 , e 2
p 1 e 1 p_1e_1 p 1 e 1 P O 2 PO_2 P O 2 I 1 I_1 I 1 p 2 e 2 p_2e_2 p 2 e 2 P O 1 PO_1 P O 1 I 1 I_1 I 1
我们现在已知p 1 , p 2 p_1,p_2 p 1 , p 2 P P P T 12 T_{12} T 1 2
将T 12 T_{12} T 1 2 R , t R,t R , t s 1 p 1 = K P , s 2 p 2 = K ( R P + t ) s_1p_1=KP,s_2p_2=K(RP+t) s 1 p 1 = K P , s 2 p 2 = K ( R P + t )
使用归一化坐标并去掉内参x 1 = K − 1 p 1 , x 2 = K − 1 p 2 x_1=K^{-1}p_1,x_2=K^{-1}p_2 x 1 = K − 1 p 1 , x 2 = K − 1 p 2 x 2 = R x 1 + t x_2=Rx_1+t x 2 = R x 1 + t
两边左乘t ^ t\hat{} t ^ t t t t ^ x 2 = t ^ R x 1 t\hat{}x_2=t\hat{}Rx_1 t ^ x 2 = t ^ R x 1
两边再左乘x 2 T x_2^T x 2 T x 2 T t ^ x 2 = x 2 T t ^ R x 1 x_2^Tt\hat{}x_2=x_2^Tt\hat{}Rx_1 x 2 T t ^ x 2 = x 2 T t ^ R x 1
左式为x 2 T ⋅ ( t × x 2 ) x_2^T \cdot (t \times x_2) x 2 T ⋅ ( t × x 2 )
故可得对极约束:x 2 T t ^ R x 1 = 0 x_2^Tt\hat{}Rx_1=0 x 2 T t ^ R x 1 = 0
表示为带内参的形式为p 2 T ( K − 1 ) T t ^ R K − 1 p 1 = 0 p_2^T{(K^{-1}})^Tt\hat{}RK^{-1}p_1=0 p 2 T ( K − 1 ) T t ^ R K − 1 p 1 = 0
R , t , P R,t,P R , t , P 定义Essential矩阵:E = t ^ R E=t\hat{}R E = t ^ R F = ( K − 1 ) T E K − 1 F={(K^{-1}})^TEK^{-1} F = ( K − 1 ) T E K − 1
由E E E E E E
由E E E E E E
常用八点法计算E E E
假设E = [ e 1 e 2 e 3 e 4 e 5 e 6 e 7 e 8 e 9 ] E=\begin{bmatrix} e_1&e_2&e_3 \\e_4&e_5&e_6\\e_7&e_8&e_9\end{bmatrix} E = ⎣ ⎢ ⎡ e 1 e 4 e 7 e 2 e 5 e 8 e 3 e 6 e 9 ⎦ ⎥ ⎤ e = [ e 1 , e 2 , ⋅ ⋅ ⋅ , e 9 ] T e=[e_1,e_2,\cdot\cdot\cdot,e_9]^T e = [ e 1 , e 2 , ⋅ ⋅ ⋅ , e 9 ] T
对于已知一对匹配点有:[ u 1 1 v 1 1 1 ] E [ u 2 1 v 2 1 1 ] = 0 \begin{bmatrix} u_{1}^1&v_{1}^1&1\end{bmatrix} E\begin{bmatrix} u_{2}^1\\v_{2}^1\\1\end{bmatrix}=0 [ u 1 1 v 1 1 1 ] E ⎣ ⎢ ⎡ u 2 1 v 2 1 1 ⎦ ⎥ ⎤ = 0
展开化简得:[ u 1 1 u 2 1 , u 1 1 v 2 1 , u 1 1 , v 1 1 u 2 1 , v 1 1 v 2 1 , v 1 1 , u 2 1 , v 2 1 , 1 ] e = 0 [u_{1}^1u_{2}^1,u_{1}^1v_{2}^1,u_{1}^1,v_{1}^1u_{2}^1,v_{1}^1v_{2}^1,v_{1}^1,u_{2}^1,v_{2}^1,1]e=0 [ u 1 1 u 2 1 , u 1 1 v 2 1 , u 1 1 , v 1 1 u 2 1 , v 1 1 v 2 1 , v 1 1 , u 2 1 , v 2 1 , 1 ] e = 0
故八点法为:
[ u 1 1 u 2 1 , u 1 1 v 2 1 , u 1 1 , v 1 1 u 2 1 , v 1 1 v 2 1 , v 1 1 , u 2 1 , v 2 1 , 1 u 1 2 u 2 2 , u 1 2 v 2 2 , u 1 2 , v 1 2 u 2 2 , v 1 2 v 2 2 , v 1 2 , u 2 2 , v 2 2 , 1 ⋅ ⋅ ⋅ u 1 8 u 2 8 , u 1 8 v 2 8 , u 1 8 , v 1 8 u 2 8 , v 1 8 v 2 8 , v 1 8 , u 2 8 , v 2 8 , 1 ] e = 0 \begin{bmatrix} u_{1}^1u_{2}^1,u_{1}^1v_{2}^1,u_{1}^1,v_{1}^1u_{2}^1,v_{1}^1v_{2}^1,v_{1}^1,u_{2}^1,v_{2}^1,1\\ u_{1}^2u_{2}^2,u_{1}^2v_{2}^2,u_{1}^2,v_{1}^2u_{2}^2,v_{1}^2v_{2}^2,v_{1}^2,u_{2}^2,v_{2}^2,1\\\ \cdot\cdot\cdot \\ u_{1}^8u_{2}^8,u_{1}^8v_{2}^8,u_{1}^8,v_{1}^8u_{2}^8,v_{1}^8v_{2}^8,v_{1}^8,u_{2}^8,v_{2}^8,1\end{bmatrix}e=0
⎣ ⎢ ⎢ ⎢ ⎡ u 1 1 u 2 1 , u 1 1 v 2 1 , u 1 1 , v 1 1 u 2 1 , v 1 1 v 2 1 , v 1 1 , u 2 1 , v 2 1 , 1 u 1 2 u 2 2 , u 1 2 v 2 2 , u 1 2 , v 1 2 u 2 2 , v 1 2 v 2 2 , v 1 2 , u 2 2 , v 2 2 , 1 ⋅ ⋅ ⋅ u 1 8 u 2 8 , u 1 8 v 2 8 , u 1 8 , v 1 8 u 2 8 , v 1 8 v 2 8 , v 1 8 , u 2 8 , v 2 8 , 1 ⎦ ⎥ ⎥ ⎥ ⎤ e = 0
求解E E E R , t R,t R , t E = t ^ R E=t\hat{}R E = t ^ R
对E E E E = U ∑ V T E=U\sum V^T E = U ∑ V T
则
t 1 ^ = U R Z ( π 2 ) ∑ U T \hat{t_1}=UR_Z(\frac{\pi}{2})\sum U^T
t 1 ^ = U R Z ( 2 π ) ∑ U T
t 2 ^ = U R Z ( − π 2 ) ∑ U T \hat{t_2}=UR_Z(-\frac{\pi}{2})\sum U^T
t 2 ^ = U R Z ( − 2 π ) ∑ U T
R 1 = U R Z T ( π 2 ) V T R_1=UR_Z^T(\frac{\pi}{2})V^T
R 1 = U R Z T ( 2 π ) V T
R 2 = U R Z T ( − π 2 ) V T R_2=UR_Z^T(-\frac{\pi}{2})V^T
R 2 = U R Z T ( − 2 π ) V T
求出四组解,通过深度为正得到真正的解。
八点法常用在单目SLAM初始化,多于八对点时,用最小二乘或者RANSAC
八点法存在的问题:尺度不确定性、纯旋转问题无法求解
八点法在特征点共面时(俯视仰视)会退化,常用单应矩阵,设特征点位于某平面− n T P d = 1 -\frac{n^TP}{d}=1 − d n T P = 1 H = K ( R − t n T d ) K − 1 H=K(R-\frac{tn^T}{d})K^{-1} H = K ( R − d t n T ) K − 1
求解完R , t R,t R , t P P P
对于s 1 x 1 = s 2 R x 2 + t s_1x_1=s_2Rx_2+t s 1 x 1 = s 2 R x 2 + t R , t , x 1 , x 2 R,t,x_1,x_2 R , t , x 1 , x 2 s 1 , s 2 s_1,s_2 s 1 , s 2
求解s 2 s_2 s 2 x 1 ^ \hat{x_1} x 1 ^ s 1 s_1 s 1 s 1 s_1 s 1
或者直接求[ − R x 2 x 1 ] [ s 2 s 1 ] = t \begin{bmatrix}-Rx_2&x_1\end{bmatrix}\begin{bmatrix}s_2\\s_1\end{bmatrix}=t [ − R x 2 x 1 ] [ s 2 s 1 ] = t
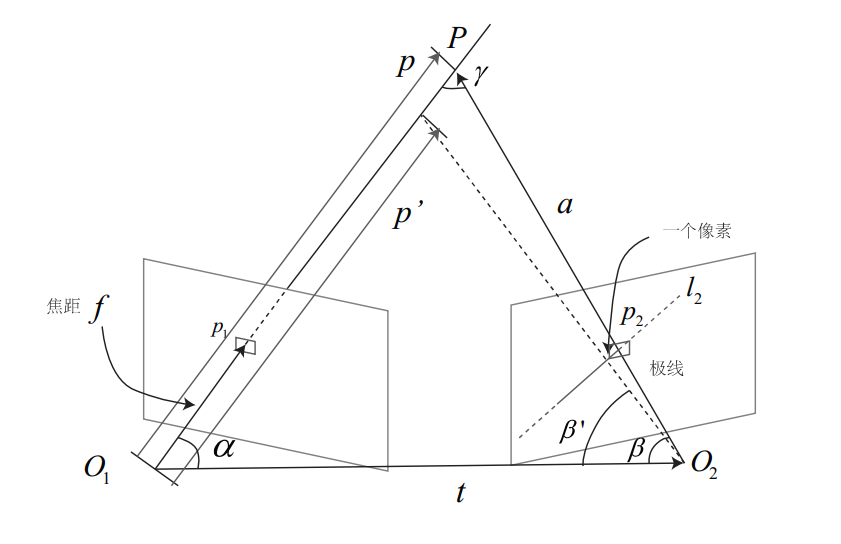
三角化存在的问题:
解得的深度的质量与平移有关,而平移太大可能导致特征匹配不成功
Pnp是已知3D点的空间位置以及在相机上的投影点,求解相机到世界的旋转和平移的方法,3D-2D。
假设世界坐标下一点P W = [ X , Y , Z , 1 ] P_W=[X,Y,Z,1] P W = [ X , Y , Z , 1 ] R P W + t RP_W+t R P W + t
假设投影点为x = [ u , v , 1 ] x=[u,v,1] x = [ u , v , 1 ] s x = R P W + t sx=RP_W+t s x = R P W + t
展开
s [ u v 1 ] = [ r 1 r 2 r 3 t 1 r 4 r 5 r 6 t 2 r 7 r 8 r 9 t 3 ] [ X Y Z 1 ] s\begin{bmatrix}u \\v \\1\end{bmatrix}=\begin{bmatrix}r_1&r_2&r_3&t_1 \\r_4&r_5&r_6&t_2 \\r_7&r_8&r_9&t_3\end{bmatrix}\begin{bmatrix}X \\Y \\Z\\1\end{bmatrix}
s ⎣ ⎢ ⎡ u v 1 ⎦ ⎥ ⎤ = ⎣ ⎢ ⎡ r 1 r 4 r 7 r 2 r 5 r 8 r 3 r 6 r 9 t 1 t 2 t 3 ⎦ ⎥ ⎤ ⎣ ⎢ ⎢ ⎢ ⎡ X Y Z 1 ⎦ ⎥ ⎥ ⎥ ⎤
最下一行s = [ r 7 , r 8 , r 9 , t 3 ] [ X , Y , Z , 1 ] T s=[r_7,r_8,r_9,t_3][X,Y,Z,1]^T s = [ r 7 , r 8 , r 9 , t 3 ] [ X , Y , Z , 1 ] T s s s
记k 1 = [ r 1 , r 2 , r 3 , t 1 ] T , k 2 = [ r 4 , r 5 , r 6 , t 2 ] T , k 3 = [ r 7 , r 8 , r 9 , t 3 ] T k_1=[r_1,r_2,r_3,t_1]^T,k_2=[r_4,r_5,r_6,t_2]^T,k_3=[r_7,r_8,r_9,t_3]^T k 1 = [ r 1 , r 2 , r 3 , t 1 ] T , k 2 = [ r 4 , r 5 , r 6 , t 2 ] T , k 3 = [ r 7 , r 8 , r 9 , t 3 ] T
则k 1 T P − k 3 T P u = 0 , k 2 T P − k 3 T P v = 0 k_1^TP-k_3^TPu=0,k_2^TP-k_3^TPv=0 k 1 T P − k 3 T P u = 0 , k 2 T P − k 3 T P v = 0
所以对于一对对应点x n = [ u n , v n , 1 ] , P n = [ X n , Y n , Z n , 1 ] T x_n=[u_n,v_n,1],P_n=[X_n,Y_n,Z_n,1]^T x n = [ u n , v n , 1 ] , P n = [ X n , Y n , Z n , 1 ] T
可以有两个方程
k 1 T P n − k 3 T P n u n = 0 k_1^TP_n-k_3^TP_nu_n=0
k 1 T P n − k 3 T P n u n = 0
k 2 T P n − k 3 T P n v n = 0 k_2^TP_n-k_3^TP_nv_n=0
k 2 T P n − k 3 T P n v n = 0
方程含有12个未知数,至少需要6对点,超过6对点用最小二乘法
该方法忽略旋转矩阵内在约束,故在求解后需要投影回S O ( 3 ) SO(3) S O ( 3 )
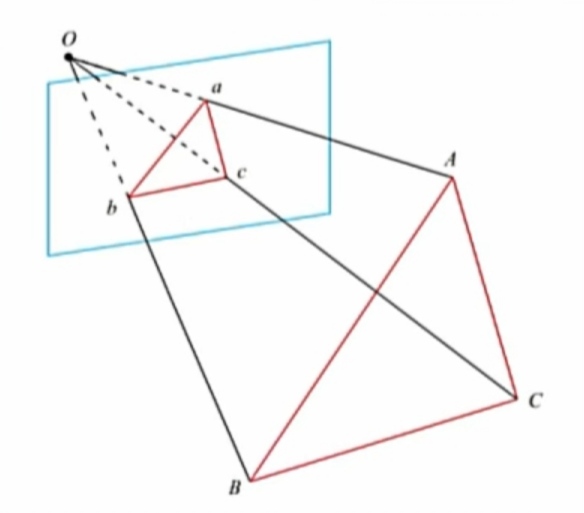
P3P需要用到4对匹配点,3对用于计算,1对用于验证
如上图,已知Δ a b c \Delta abc Δ a b c Δ A B C \Delta ABC Δ A B C
我们需要求解出Δ A B C \Delta ABC Δ A B C P n P PnP P n P I C P ICP I C P
由相似可得
O A 2 + O B 2 − 2 O A ⋅ O B c o s ( a , b ) = A B 2 OA^2+OB^2-2OA\cdot OBcos(a,b)=AB^2
O A 2 + O B 2 − 2 O A ⋅ O B c o s ( a , b ) = A B 2
O B 2 + O C 2 − 2 O B ⋅ O C c o s ( b , c ) = B C 2 OB^2+OC^2-2OB\cdot OCcos(b,c)=BC^2
O B 2 + O C 2 − 2 O B ⋅ O C c o s ( b , c ) = B C 2
O A 2 + O C 2 − 2 O A ⋅ O C c o s ( a , c ) = A C 2 OA^2+OC^2-2OA\cdot OCcos(a,c)=AC^2
O A 2 + O C 2 − 2 O A ⋅ O C c o s ( a , c ) = A C 2
三式除以O C 2 OC^2 O C 2 x = O A O C , y = O B O C x=\frac{OA}{OC},y=\frac{OB}{OC} x = O C O A , y = O C O B
x 2 + y 2 − 2 x y c o s ( a , b ) = A B 2 O C 2 x^2+y^2-2xycos(a,b)=\frac{AB^2}{OC^2}
x 2 + y 2 − 2 x y c o s ( a , b ) = O C 2 A B 2
x 2 + 1 − 2 y c o s ( b , c ) = B C 2 O C 2 x^2+1-2ycos(b,c)=\frac{BC^2}{OC^2}
x 2 + 1 − 2 y c o s ( b , c ) = O C 2 B C 2
x 2 + 1 − 2 x c o s ( a , c ) = A C 2 O C 2 x^2+1-2xcos(a,c)=\frac{AC^2}{OC^2}
x 2 + 1 − 2 x c o s ( a , c ) = O C 2 A C 2
记v = A B 2 O C 2 , u = B C 2 A B 2 , w = A C 2 A B 2 v=\frac{AB^2}{OC^2},u=\frac{BC^2}{AB^2},w=\frac{AC^2}{AB^2} v = O C 2 A B 2 , u = A B 2 B C 2 , w = A B 2 A C 2
x 2 + y 2 − 2 x y c o s ( a , b ) = v x^2+y^2-2xycos(a,b)=v
x 2 + y 2 − 2 x y c o s ( a , b ) = v
x 2 + 1 − 2 y c o s ( b , c ) − u v = 0 x^2+1-2ycos(b,c)-uv=0
x 2 + 1 − 2 y c o s ( b , c ) − u v = 0
x 2 + 1 − 2 x c o s ( a , c ) − w v = 0 x^2+1-2xcos(a,c)-wv=0
x 2 + 1 − 2 x c o s ( a , c ) − w v = 0
把第一式带入下面两个式子得
x 2 + 1 − 2 y c o s ( b , c ) − u ( x 2 + y 2 − 2 x y c o s ( a , b ) ) = 0 x^2+1-2ycos(b,c)-u(x^2+y^2-2xycos(a,b))=0
x 2 + 1 − 2 y c o s ( b , c ) − u ( x 2 + y 2 − 2 x y c o s ( a , b ) ) = 0
x 2 + 1 − 2 x c o s ( a , c ) − w ( x 2 + y 2 − 2 x y c o s ( a , b ) ) = 0 x^2+1-2xcos(a,c)-w(x^2+y^2-2xycos(a,b))=0
x 2 + 1 − 2 x c o s ( a , c ) − w ( x 2 + y 2 − 2 x y c o s ( a , b ) ) = 0
其中c o s , u , w cos,u,w c o s , u , w x , y x,y x , y x , y x,y x , y
故我们解得Δ A B C \Delta ABC Δ A B C
P3P缺点:多于3对匹配点难以处理、没法处理误匹配
Bundle Adjustment是PnP的一种优化解法
投影关系表示为李代数:s u = K e x p ( ξ ^ ) P su=Kexp(\xi \hat{})P s u = K e x p ( ξ ^ ) P
则e i = u i − 1 s i K e x p ( ξ ^ ) P i e_i =u_i-\frac{1}{s_i}Kexp(\xi\hat{})P_i e i = u i − s i 1 K e x p ( ξ ^ ) P i u i u_i u i
定义重投影误差ξ ∗ = a r g m i n ( 1 2 ∑ i = 1 n ∣ ∣ u i − 1 s i K e x p ( ξ ^ ) P i ∣ ∣ 2 2 ) \xi^*=argmin(\frac{1}{2}\sum^n_{i=1}{\vert\vert u_i-\frac{1}{s_i}Kexp(\xi\hat{})P_i\vert\vert_2}^2) ξ ∗ = a r g m i n ( 2 1 ∑ i = 1 n ∣ ∣ u i − s i 1 K e x p ( ξ ^ ) P i ∣ ∣ 2 2 )
则∂ e ∂ δ ξ = lim δ ξ → 0 e ( δ ξ + ξ ) δ ξ = ∂ e ∂ P ′ ∂ P ′ ∂ δ ξ \frac{\partial e}{\partial \delta\xi}=\lim_{\delta\xi \rightarrow 0}\frac{e(\delta\xi+\xi)}{\delta\xi}=\frac{\partial e}{\partial P'}\frac{\partial P'}{\partial \delta \xi} ∂ δ ξ ∂ e = lim δ ξ → 0 δ ξ e ( δ ξ + ξ ) = ∂ P ′ ∂ e ∂ δ ξ ∂ P ′ P ′ = e x p ( ξ ^ ) P P'=exp(\xi\hat{})P P ′ = e x p ( ξ ^ ) P
先求∂ e ∂ P ′ \frac{\partial e}{\partial P'} ∂ P ′ ∂ e
∂ e ∂ P ′ = − [ ∂ u ∂ X ′ ∂ u ∂ Y ′ ∂ u ∂ Z ′ ∂ v ∂ X ′ ∂ v ∂ Y ′ ∂ v ∂ Z ′ ] \frac{\partial e}{\partial P'}=-\begin{bmatrix} \frac{\partial u}{\partial X'}&\frac{\partial u}{\partial Y'}&\frac{\partial u}{\partial Z'}\\\frac{\partial v}{\partial X'}&\frac{\partial v}{\partial Y'}&\frac{\partial v}{\partial Z'}\end{bmatrix} ∂ P ′ ∂ e = − [ ∂ X ′ ∂ u ∂ X ′ ∂ v ∂ Y ′ ∂ u ∂ Y ′ ∂ v ∂ Z ′ ∂ u ∂ Z ′ ∂ v ]
而u = f x X ′ Z ′ + c x , v = f y Y ′ Z ′ + c y u= f_x \frac{X'}{Z'}+c_x ,v = f_y \frac{Y'}{Z'}+c_y u = f x Z ′ X ′ + c x , v = f y Z ′ Y ′ + c y
故∂ e ∂ P ′ = − [ f x Z ′ 0 − f x X ′ Z ′ 2 0 f y Z ′ − f y Y ′ Z ′ 2 ] \frac{\partial e}{\partial P'}=-\begin{bmatrix}\frac{f_x}{Z'}&0&-\frac{f_xX'}{Z'^2}\\0&\frac{f_y}{Z'}&-\frac{f_yY'}{Z'^2}\end{bmatrix} ∂ P ′ ∂ e = − [ Z ′ f x 0 0 Z ′ f y − Z ′ 2 f x X ′ − Z ′ 2 f y Y ′ ]
再求∂ P ′ ∂ δ ξ \frac{\partial P'}{\partial \delta \xi} ∂ δ ξ ∂ P ′
对于S E ( 3 ) SE(3) S E ( 3 ) ξ \xi ξ p p p T = [ R t 0 1 ] T=\begin{bmatrix} R & t \\ 0 &1\end{bmatrix} T = [ R 0 t 1 ]
扰动模型:∂ ( T p ) ∂ ξ = [ I − ( R p + t ) ^ 0 T 0 T ] \frac{\partial (Tp)}{\partial \xi} =\begin{bmatrix} I & -(Rp+t) \hat{} \\ 0^T & 0 ^T \end{bmatrix} ∂ ξ ∂ ( T p ) = [ I 0 T − ( R p + t ) ^ 0 T ]
这里P ′ P' P ′ ∂ P ′ ∂ δ ξ = [ I , − P ′ ^ ] = [ 1 0 0 0 Z ′ − Y ′ 0 1 0 − Z ′ 0 X ′ 0 0 1 Y ′ − X ′ 0 ] \frac{\partial P'}{\partial \delta \xi}=[I , -P'\hat{}]=\begin{bmatrix}1&0&0&0&Z'&-Y' \\0&1&0&-Z'&0&X'\\0&0&1&Y'&-X'&0\end{bmatrix} ∂ δ ξ ∂ P ′ = [ I , − P ′ ^ ] = ⎣ ⎢ ⎡ 1 0 0 0 1 0 0 0 1 0 − Z ′ Y ′ Z ′ 0 − X ′ − Y ′ X ′ 0 ⎦ ⎥ ⎤
相乘整合可得
∂ e ∂ δ ξ = ∂ e ∂ P ′ ∂ P ′ ∂ δ ξ = − [ f x Z ′ 0 − f x X ′ Z ′ 2 − f x X ′ Y ′ Z ′ 2 f x + f x X ′ 2 Z ′ 2 − f x Y ′ Z ′ 0 f y Z ′ − f y Y ′ Z ′ 2 − f y − f y Y ′ 2 Z ′ 2 f y X ′ Y ′ Z ′ 2 f y X ′ Z ′ ] \frac{\partial e}{\partial \delta\xi}=\frac{\partial e}{\partial P'}\frac{\partial P'}{\partial \delta \xi}=-\begin{bmatrix} \frac{f_x}{Z'}&0&-\frac{f_xX'}{Z'^2}&-\frac{f_xX'Y'}{Z'^2}&f_x+\frac{f_xX'^2}{Z'^2}&-\frac{f_xY'}{Z'} \\ 0&\frac{f_y}{Z'}&-\frac{f_yY'}{Z'^2}&-f_y-\frac{f_yY'^2}{Z'^2}&\frac{f_yX'Y'}{Z'^2}&\frac{f_yX'}{Z'}\end{bmatrix} ∂ δ ξ ∂ e = ∂ P ′ ∂ e ∂ δ ξ ∂ P ′ = − [ Z ′ f x 0 0 Z ′ f y − Z ′ 2 f x X ′ − Z ′ 2 f y Y ′ − Z ′ 2 f x X ′ Y ′ − f y − Z ′ 2 f y Y ′ 2 f x + Z ′ 2 f x X ′ 2 Z ′ 2 f y X ′ Y ′ − Z ′ f x Y ′ Z ′ f y X ′ ]
同理可以对P P P ∂ e ∂ P = − [ f x Z ′ 0 − f x X ′ Z ′ 2 0 f y Z ′ − f y Y ′ Z ′ 2 ] R \frac{\partial e}{\partial P}=-\begin{bmatrix}\frac{f_x}{Z'}&0&-\frac{f_xX'}{Z'^2}\\0&\frac{f_y}{Z'}&-\frac{f_yY'}{Z'^2}\end{bmatrix}R ∂ P ∂ e = − [ Z ′ f x 0 0 Z ′ f y − Z ′ 2 f x X ′ − Z ′ 2 f y Y ′ ] R
常用于RGBD相机,3D-3D
假设已知空间中一些点在相机一的坐标为P = { p 1 , p 2 , ⋅ ⋅ ⋅ , p n } P=\{p_1,p_2,\cdot\cdot\cdot,p_n\} P = { p 1 , p 2 , ⋅ ⋅ ⋅ , p n }
同样的点在相机二的坐标为P ′ = { p 1 ′ , p 2 ′ , ⋅ ⋅ ⋅ , p n ′ } P'=\{p_1',p_2',\cdot\cdot\cdot,p_n'\} P ′ = { p 1 ′ , p 2 ′ , ⋅ ⋅ ⋅ , p n ′ }
那么它们之间满足P = R P ′ + t P=RP'+t P = R P ′ + t
定义误差项e i = p i − ( R p i ′ + t ) e_i=p_i-(Rp_i'+t) e i = p i − ( R p i ′ + t )
故有最小二乘问题min R , t J = 1 2 ∑ i = 1 n ∣ ∣ p i − ( R p i ′ + t ) ∣ ∣ 2 2 \min_{R,t} \, J=\frac{1}{2}\sum_{i=1}^n{\vert\vert p_i-(Rp_i'+t)\vert\vert_2}^2 min R , t J = 2 1 ∑ i = 1 n ∣ ∣ p i − ( R p i ′ + t ) ∣ ∣ 2 2
定义质心:p = 1 n ∑ i = 1 n p i , p ′ = 1 n ∑ i = 1 n p i ′ p=\frac{1}{n}\sum_{i=1}^np_i,p'=\frac{1}{n}\sum_{i=1}^np_i' p = n 1 ∑ i = 1 n p i , p ′ = n 1 ∑ i = 1 n p i ′
故可以修改目标函数如下:
J = 1 2 ∑ i = 1 n ∣ ∣ p i − ( R p i ′ + t ) + ( p − p ) + ( R p ′ − R p ′ ) ∣ ∣ 2 = 1 2 ∑ i = 1 n ∣ ∣ p i − p − ( R p i ′ − R p ′ ) + ( p − R p ′ − t ) ∣ ∣ 2 = 1 2 ∑ i = 1 n ∣ ∣ p i − p − ( R p i ′ − R p ′ ) ∣ ∣ 2 + ∣ ∣ ( p − R p ′ − t ) ∣ ∣ 2 J=\frac{1}{2}\sum_{i=1}^n{\vert\vert p_i-(Rp_i'+t)+(p-p)+(Rp'-Rp')\vert\vert}^2 \\
= \frac{1}{2}\sum_{i=1}^n{\vert\vert p_i-p-(Rp_i'-Rp')+(p-Rp'-t)\vert\vert}^2 \\
=\frac{1}{2}\sum_{i=1}^n{\vert\vert p_i-p-(Rp_i'-Rp')\vert\vert^2+\vert\vert(p-Rp'-t)\vert\vert}^2
J = 2 1 i = 1 ∑ n ∣ ∣ p i − ( R p i ′ + t ) + ( p − p ) + ( R p ′ − R p ′ ) ∣ ∣ 2 = 2 1 i = 1 ∑ n ∣ ∣ p i − p − ( R p i ′ − R p ′ ) + ( p − R p ′ − t ) ∣ ∣ 2 = 2 1 i = 1 ∑ n ∣ ∣ p i − p − ( R p i ′ − R p ′ ) ∣ ∣ 2 + ∣ ∣ ( p − R p ′ − t ) ∣ ∣ 2
其中平方和展开交叉相乘项为0,J J J R R R R , t R,t R , t
采取解的方式为最小化左边项获得R R R t t t
故需要求解min R R ∗ = 1 2 ∑ i = 1 n ∣ ∣ p i − p − ( R p i ′ − R p ′ ) ∣ ∣ 2 \min_R \, R^*=\frac{1}{2}\sum_{i=1}^n{\vert\vert p_i-p-(Rp_i'-Rp')\vert\vert}^2 min R R ∗ = 2 1 ∑ i = 1 n ∣ ∣ p i − p − ( R p i ′ − R p ′ ) ∣ ∣ 2
定义去质心坐标:q i = p i − p , q i ′ = p i ′ − p ′ q_i=p_i-p,q_i'=p_i'-p' q i = p i − p , q i ′ = p i ′ − p ′
故可以修改目标函数如下:
R ∗ = 1 2 ∑ i = 1 n ∣ ∣ p i − p − ( R p i ′ − R p ′ ) ∣ ∣ 2 = 1 2 ∑ i = 1 n ∣ ∣ q i − R q i ′ ∣ ∣ 2 = 1 2 ∑ i = 1 n q i T q i + q i ′ T R T R q i ′ − 2 q i T R q i ′ R^*=\frac{1}{2}\sum_{i=1}^n{\vert\vert p_i-p-(Rp_i'-Rp')\vert\vert}^2 \\
=\frac{1}{2}\sum_{i=1}^n{\vert\vert q_i-Rq_i'\vert\vert}^2\\
=\frac{1}{2}\sum_{i=1}^n{q_i^Tq_i+q_i'^TR^TRq_i'-2q_i^TRq_i'}
R ∗ = 2 1 i = 1 ∑ n ∣ ∣ p i − p − ( R p i ′ − R p ′ ) ∣ ∣ 2 = 2 1 i = 1 ∑ n ∣ ∣ q i − R q i ′ ∣ ∣ 2 = 2 1 i = 1 ∑ n q i T q i + q i ′ T R T R q i ′ − 2 q i T R q i ′
只有最后一项与R R R
− ∑ i = 1 n q i T R q i ′ = − ∑ i = 1 n t r ( R q i ′ q i T ) = − t r ( R ∑ i = 1 n q i ′ q i T ) -\sum_{i=1}^nq_i^TRq_i'=-\sum_{i=1}^ntr(Rq_i'q_i^T)=-tr(R\sum_{i=1}^nq_i'q_i^T) − ∑ i = 1 n q i T R q i ′ = − ∑ i = 1 n t r ( R q i ′ q i T ) = − t r ( R ∑ i = 1 n q i ′ q i T )
可以通过SVD求解
求W = ∑ i = 1 n q i q i ′ T W=\sum_{i=1}^nq_iq_i'^T W = ∑ i = 1 n q i q i ′ T U ∑ V T U\sum V^T U ∑ V T R = U V T R=UV^T R = U V T
求完R R R t = p − R p ′ t=p-Rp' t = p − R p ′
同理,ICP也可以通过非线性优化求解
∂ e ∂ δ ξ = ∂ e ∂ P ′ ∂ P ′ ∂ δ ξ = − I ∂ P ′ ∂ δ ξ = − I [ I , − P ′ ^ ] = [ − 1 0 0 0 − Z ′ Y ′ 0 − 1 0 Z ′ 0 − X ′ 0 0 − 1 − Y ′ X ′ 0 ] \frac{\partial e}{\partial \delta\xi}=\frac{\partial e}{\partial P'}\frac{\partial P'}{\partial \delta \xi}=-I\frac{\partial P'}{\partial \delta \xi}=-I[I , -P'\hat{}]=\begin{bmatrix}-1&0&0&0&-Z'&Y' \\0&-1&0&Z'&0&-X'\\0&0&-1&-Y'&X'&0\end{bmatrix} ∂ δ ξ ∂ e = ∂ P ′ ∂ e ∂ δ ξ ∂ P ′ = − I ∂ δ ξ ∂ P ′ = − I [ I , − P ′ ^ ] = ⎣ ⎢ ⎡ − 1 0 0 0 − 1 0 0 0 − 1 0 Z ′ − Y ′ − Z ′ 0 X ′ Y ′ − X ′ 0 ⎦ ⎥ ⎤
稀疏光流以LK光流为代表,稠密光流以HS光流为代表
实际就是通过光流的方法找到匹配点
假设在t t t ( x , y ) (x,y) ( x , y ) I ( x , y , t ) I(x,y,t) I ( x , y , t )
在t + Δ t t+\Delta t t + Δ t ( x + Δ x , y + Δ y ) (x+\Delta x,y+\Delta y) ( x + Δ x , y + Δ y ) I ( x + Δ x , y + Δ y , t + Δ t ) I(x+\Delta x,y+\Delta y,t+\Delta t) I ( x + Δ x , y + Δ y , t + Δ t )
由灰度不变性可得I ( x , y , t ) = I ( x + Δ x , y + Δ y , t + Δ t ) I(x,y,t) = I(x+\Delta x,y+\Delta y,t+\Delta t) I ( x , y , t ) = I ( x + Δ x , y + Δ y , t + Δ t )
泰勒展开I ( x + Δ x , y + Δ y , t + Δ t ) ≈ I ( x , y , t ) + ∂ I ∂ x d x + ∂ I ∂ y d y + ∂ I ∂ t d t I(x+\Delta x,y+\Delta y,t+\Delta t) \approx I(x,y,t)+\frac{\partial I}{\partial x}dx+\frac{\partial I}{\partial y}dy+\frac{\partial I}{\partial t}dt I ( x + Δ x , y + Δ y , t + Δ t ) ≈ I ( x , y , t ) + ∂ x ∂ I d x + ∂ y ∂ I d y + ∂ t ∂ I d t
所以∂ I ∂ x d x + ∂ I ∂ y d y + ∂ I ∂ t d t = 0 \frac{\partial I}{\partial x}dx+\frac{\partial I}{\partial y}dy+\frac{\partial I}{\partial t}dt = 0 ∂ x ∂ I d x + ∂ y ∂ I d y + ∂ t ∂ I d t = 0 ∂ I ∂ x d x d t + ∂ I ∂ y d y d t = − ∂ I ∂ t \frac{\partial I}{\partial x}\frac{dx}{dt}+\frac{\partial I}{\partial y}\frac{dy}{dt}=-\frac{\partial I}{\partial t} ∂ x ∂ I d t d x + ∂ y ∂ I d t d y = − ∂ t ∂ I
其中∂ I ∂ x , ∂ I ∂ y , − ∂ I ∂ t \frac{\partial I}{\partial x},\frac{\partial I}{\partial y},-\frac{\partial I}{\partial t} ∂ x ∂ I , ∂ y ∂ I , − ∂ t ∂ I d x d t , d y d t \frac{dx}{dt},\frac{dy}{dt} d t d x , d t d y
常取假设一个窗口W × W W \times W W × W
记∂ I ∂ x = I x , ∂ I ∂ y = I y , ∂ I ∂ t = I t , d x d t = u , d y d t = v \frac{\partial I}{\partial x}=I_x,\frac{\partial I}{\partial y}=I_y,\frac{\partial I}{\partial t}=I_t,\frac{dx}{dt}=u,\frac{dy}{dt}=v ∂ x ∂ I = I x , ∂ y ∂ I = I y , ∂ t ∂ I = I t , d t d x = u , d t d y = v
则有[ I x 1 , I y 1 I x 2 , I y 2 ⋅ ⋅ ⋅ I x n , I y n ] [ u v ] = [ − I t 1 − I t 2 ⋅ ⋅ ⋅ − I t n ] \begin{bmatrix} I_x^1,I_y^1\\I_x^2,I_y^2 \\ \cdot\cdot\cdot \\I_x^n,I_y^n\end{bmatrix}\begin{bmatrix} u\\ v\end{bmatrix}=\begin{bmatrix}-I_t^1\\-I_t^2\\ \cdot\cdot\cdot\\-I_t^n\end{bmatrix} ⎣ ⎢ ⎢ ⎢ ⎡ I x 1 , I y 1 I x 2 , I y 2 ⋅ ⋅ ⋅ I x n , I y n ⎦ ⎥ ⎥ ⎥ ⎤ [ u v ] = ⎣ ⎢ ⎢ ⎢ ⎡ − I t 1 − I t 2 ⋅ ⋅ ⋅ − I t n ⎦ ⎥ ⎥ ⎥ ⎤ A [ u v ] = b A\begin{bmatrix}u\\v\end{bmatrix}=b A [ u v ] = b
则[ u v ] ∗ = − ( A T A ) − 1 A T b \begin{bmatrix}u\\v\end{bmatrix}^* = -(A^TA)^{-1}A^Tb [ u v ] ∗ = − ( A T A ) − 1 A T b
光流法没有用到相机本身的几何结构,没有考虑相机的旋转而缩放,而直接法考虑了这些信息
假设空间中一点P P P p 1 p_1 p 1 p 2 p_2 p 2
假设第一帧到第二帧的初始估计为R , t R,t R , t
则有p 1 = 1 Z 1 K P , p 2 = 1 Z 2 K ( R P + t ) = 1 Z 2 K e x p ( ξ ^ ) P p_1=\frac{1}{Z_1}KP,p_2=\frac{1}{Z_2}K(RP+t)=\frac{1}{Z_2}Kexp(\xi\hat{})P p 1 = Z 1 1 K P , p 2 = Z 2 1 K ( R P + t ) = Z 2 1 K e x p ( ξ ^ ) P
定义光度误差e = I 1 ( p 1 ) − I 2 ( p 2 ) e=I_1(p_1)-I_2(p_2) e = I 1 ( p 1 ) − I 2 ( p 2 )
故有最小二乘问题min ξ J = ∑ i = 1 N e i T e i \min_{\xi} \, J=\sum_{i=1}^Ne_i^Te_i min ξ J = ∑ i = 1 N e i T e i
根据扰动模型得
e ( ξ ⊕ δ ξ ) = I 1 ( 1 Z 1 K P ) − I 2 ( 1 Z 2 K e x p ( δ ξ ^ ) e x p ( ξ ^ ) P ) ≈ I 1 ( 1 Z 1 K P ) − I 2 ( 1 Z 2 K ( 1 + δ ξ ^ ) e x p ( ξ ^ ) P ) = I 1 ( 1 Z 1 K P ) − I 2 ( 1 Z 2 K e x p ( ξ ^ ) P + 1 Z 2 K δ ξ ^ e x p ( ξ ^ ) P ) e(\xi \, \oplus \delta\xi)=I_1(\frac{1}{Z_1}KP)-I_2(\frac{1}{Z_2}Kexp(\delta\xi\hat{})exp(\xi\hat{})P) \\
\approx I_1(\frac{1}{Z_1}KP)-I_2(\frac{1}{Z_2}K(1+\delta\xi\hat{})exp(\xi\hat{})P)\\
=I_1(\frac{1}{Z_1}KP)-I_2(\frac{1}{Z_2}Kexp(\xi\hat{})P+\frac{1}{Z_2}K\delta\xi\hat{}exp(\xi\hat{})P)\\
e ( ξ ⊕ δ ξ ) = I 1 ( Z 1 1 K P ) − I 2 ( Z 2 1 K e x p ( δ ξ ^ ) e x p ( ξ ^ ) P ) ≈ I 1 ( Z 1 1 K P ) − I 2 ( Z 2 1 K ( 1 + δ ξ ^ ) e x p ( ξ ^ ) P ) = I 1 ( Z 1 1 K P ) − I 2 ( Z 2 1 K e x p ( ξ ^ ) P + Z 2 1 K δ ξ ^ e x p ( ξ ^ ) P )
记q = δ ξ ^ e x p ( ξ ^ ) P , u = 1 Z 2 K q q =\delta\xi\hat{}exp(\xi\hat{})P,u=\frac{1}{Z_2}Kq q = δ ξ ^ e x p ( ξ ^ ) P , u = Z 2 1 K q
e ( ξ ⊕ δ ξ ) = I 1 ( 1 Z 1 K P ) − I 2 ( 1 Z 2 K e x p ( ξ ^ ) P + u ) = I 1 ( 1 Z 1 K P ) − I 2 ( 1 Z 2 K e x p ( ξ ^ ) P ) − ∂ I 2 ∂ u ∂ u ∂ q ∂ q ∂ δ ξ δ ξ = e ( ξ ) − ∂ I 2 ∂ u ∂ u ∂ q ∂ q ∂ δ ξ δ ξ e(\xi \, \oplus \delta\xi)
=I_1(\frac{1}{Z_1}KP)-I_2(\frac{1}{Z_2}Kexp(\xi\hat{})P+u) \\
=I_1(\frac{1}{Z_1}KP)-I_2(\frac{1}{Z_2}Kexp(\xi\hat{})P)-\frac{\partial I_2}{\partial u} \frac{\partial u}{\partial q} \frac{\partial q}{\partial \delta \xi}\delta\xi \\
=e(\xi)-\frac{\partial I_2}{\partial u} \frac{\partial u}{\partial q} \frac{\partial q}{\partial \delta \xi}\delta\xi
e ( ξ ⊕ δ ξ ) = I 1 ( Z 1 1 K P ) − I 2 ( Z 2 1 K e x p ( ξ ^ ) P + u ) = I 1 ( Z 1 1 K P ) − I 2 ( Z 2 1 K e x p ( ξ ^ ) P ) − ∂ u ∂ I 2 ∂ q ∂ u ∂ δ ξ ∂ q δ ξ = e ( ξ ) − ∂ u ∂ I 2 ∂ q ∂ u ∂ δ ξ ∂ q δ ξ
其中
∂ I 2 ∂ u \frac{\partial I_2}{\partial u} ∂ u ∂ I 2 ∂ u ∂ q \frac{\partial u}{\partial q} ∂ q ∂ u ∂ q ∂ δ ξ \frac{\partial q}{\partial \delta \xi} ∂ δ ξ ∂ q
∂ u ∂ δ ξ \frac{\partial u}{\partial \delta \xi} ∂ δ ξ ∂ u
J = − ∂ I 2 ∂ u ∂ u ∂ δ ξ = − ∂ I 2 ∂ u [ f x Z 0 − f x X Z 2 − f x X Y Z 2 f x + f x X 2 Z 2 − f x Y Z 0 f y Z − f y Y Z 2 − f y − f y Y 2 Z 2 f y X Y Z 2 f y X Z ] J=-\frac{\partial I_2}{\partial u}\frac{\partial u}{\partial \delta \xi}=-\frac{\partial I_2}{\partial u}\begin{bmatrix} \frac{f_x}{Z}&0&-\frac{f_xX}{Z^2}&-\frac{f_xXY}{Z^2}&f_x+\frac{f_xX^2}{Z^2}&-\frac{f_xY}{Z} \\ 0&\frac{f_y}{Z}&-\frac{f_yY}{Z^2}&-f_y-\frac{f_yY^2}{Z^2}&\frac{f_yXY}{Z^2}&\frac{f_yX}{Z}\end{bmatrix}
J = − ∂ u ∂ I 2 ∂ δ ξ ∂ u = − ∂ u ∂ I 2 [ Z f x 0 0 Z f y − Z 2 f x X − Z 2 f y Y − Z 2 f x X Y − f y − Z 2 f y Y 2 f x + Z 2 f x X 2 Z 2 f y X Y − Z f x Y Z f y X ]
补充一点双线性插值
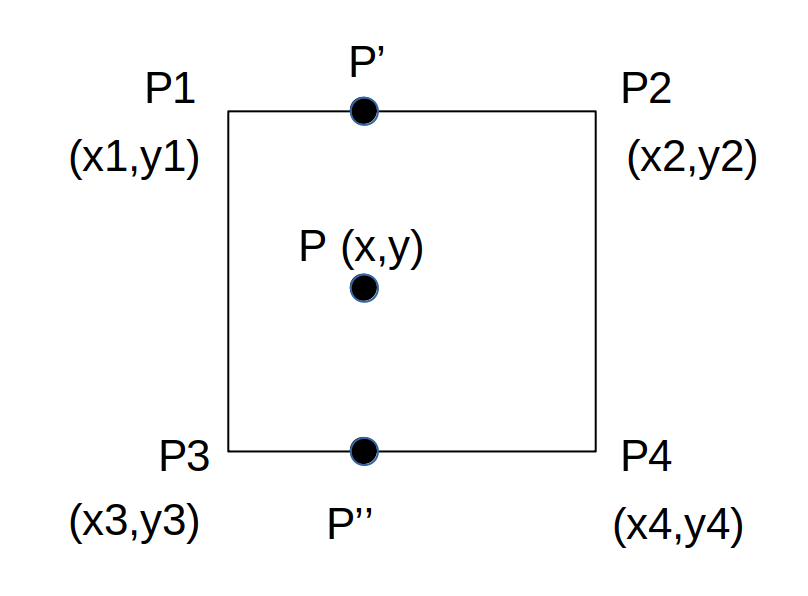
如图,我们已知四个相邻的像素点P 1 , P 2 , P 3 , P 4 P_1,P_2,P_3,P_4 P 1 , P 2 , P 3 , P 4
现在估算浮点数坐标P P P
先算P ′ P' P ′ P ′ ′ P'' P ′ ′
记Δ x = x − x 1 , Δ y = y − y 1 \Delta x =x-x_1,\Delta y = y-y_1 Δ x = x − x 1 , Δ y = y − y 1
I ( P ′ ) ≈ Δ x I ( P 2 ) + ( 1 − Δ x ) I ( P 1 ) I(P') \approx\Delta xI(P_2)+(1-\Delta x)I(P_1)
I ( P ′ ) ≈ Δ x I ( P 2 ) + ( 1 − Δ x ) I ( P 1 )
I ( P ′ ′ ) ≈ Δ x I ( P 4 ) + ( 1 − Δ x ) I ( P 3 ) I(P'') \approx\Delta xI(P_4)+(1-\Delta x)I(P_3)
I ( P ′ ′ ) ≈ Δ x I ( P 4 ) + ( 1 − Δ x ) I ( P 3 )
而
I ( P ) ≈ Δ y I ( P ′ ′ ) + ( 1 − Δ y ) I ( P ′ ) I(P) \approx\Delta y I(P'')+(1-\Delta y)I(P') \\
I ( P ) ≈ Δ y I ( P ′ ′ ) + ( 1 − Δ y ) I ( P ′ )
所以
I ( P ) = Δ y [ Δ x I ( P 4 ) + ( 1 − Δ x ) I ( P 3 ) ] + ( 1 − Δ y ) [ Δ x I ( P 2 ) + ( 1 − Δ x ) I ( P 1 ) ] I(P) =\Delta y[\Delta xI(P_4)+(1-\Delta x)I(P_3)]+
(1-\Delta y)[\Delta xI(P_2)+(1-\Delta x)I(P_1)] \\
I ( P ) = Δ y [ Δ x I ( P 4 ) + ( 1 − Δ x ) I ( P 3 ) ] + ( 1 − Δ y ) [ Δ x I ( P 2 ) + ( 1 − Δ x ) I ( P 1 ) ]
整理得
I ( P ) = ( 1 − Δ x ) ( 1 − Δ y ) I ( P 1 ) + Δ x ( 1 − Δ y ) I ( P 2 ) + ( 1 − Δ x ) ( Δ y ) I ( P 3 ) + Δ x Δ y I ( P 4 ) I(P)=(1-\Delta x)(1-\Delta y)I(P_1)+\Delta x(1-\Delta y)I(P_2)+(1-\Delta x)(\Delta y)I(P_3)+\Delta x\Delta yI(P_4)
I ( P ) = ( 1 − Δ x ) ( 1 − Δ y ) I ( P 1 ) + Δ x ( 1 − Δ y ) I ( P 2 ) + ( 1 − Δ x ) ( Δ y ) I ( P 3 ) + Δ x Δ y I ( P 4 )
viz可以用于位姿可视化
先检查opencv的modules目录下有没有viz文件夹
没有的话下载对应OpenCV版本的opencv_contrib并解压,比如我是4.5.0
网址:https://github.com/opencv/opencv_contrib/tags
sudo apt-get install libvtk6-dev # 依赖 不同ubuntu版本不同
cp -r opencv_contrib-4.5.0/modules/viz/ opencv-4.5.0/modules/ # 拷贝 我们只需要其中的viz
cd opencv-4.5.0/build
cmake -DWITH_VTK=ON ..
make
sudo make install
之前opencv3时使用viz不需要额外引入头文件
换用opencv4使用时需要包含opencv2/viz.hpp
数据集:http://vision.in.tum.de/data/datasets/rgbd-dataset/download
对于运动方程和观测方程:
x k = f ( x k − 1 , u k ) + w k x_k=f(x_{k-1},u_k)+w_k x k = f ( x k − 1 , u k ) + w k
z k , j = h ( y j , x k ) + v k , j z_{k,j}=h(y_j,x_k)+v_{k,j} z k , j = h ( y j , x k ) + v k , j
我们将k k k T k ≜ { x k , y 1 , . . . , y m } T_k\triangleq \{x_k,y_1,...,y_m\} T k ≜ { x k , y 1 , . . . , y m } T T T x x x y y y
则运动方程和观测方程化简为:
T k = f ( T k − 1 , u k ) + w k T_k = f(T_{k-1},u_k)+w_k T k = f ( T k − 1 , u k ) + w k
z k = h ( T k ) + v k z_k = h(T_k)+v_k z k = h ( T k ) + v k
我们需要估计的当前状态为P ( T k ∣ T 0 , u 1 : k , z 1 : k ) P(T_k \vert T_0,u_{1:k},z_{1:k}) P ( T k ∣ T 0 , u 1 : k , z 1 : k )
根据贝叶斯公式P ( A ∣ B ) = P ( B ∣ A ) P ( A ) P ( B ) P(A \vert B) = \frac{P(B \vert A) P(A)}{P(B)} P ( A ∣ B ) = P ( B ) P ( B ∣ A ) P ( A ) P ( T k ∣ T 0 , u 1 : k , z 1 : k ) ∝ P ( z k ∣ T k ) P ( T k ∣ T 0 , u 1 : k , z 1 : k − 1 ) P(T_k \vert T_0,u_{1:k},z_{1:k}) \propto P(z_k \vert T_k) P(T_k \vert T_0,u_{1:k},z_{1:k-1}) P ( T k ∣ T 0 , u 1 : k , z 1 : k ) ∝ P ( z k ∣ T k ) P ( T k ∣ T 0 , u 1 : k , z 1 : k − 1 )
其中P ( z k ∣ T k ) P(z_k \vert T_k) P ( z k ∣ T k ) P ( T k ∣ T 0 , u 1 : k , z 1 : k − 1 ) P(T_k \vert T_0,u_{1:k},z_{1:k-1}) P ( T k ∣ T 0 , u 1 : k , z 1 : k − 1 )
对先验进行展开:
P ( T k ∣ T 0 , u 1 : k , z 1 : k − 1 ) = ∫ P ( T k ∣ T k − 1 , T 0 , u 1 : k , z 1 : k − 1 ) P ( T k − 1 ∣ T 0 , u 1 : k , z 1 : k − 1 ) d T k − 1 P(T_k \vert T_0,u_{1:k},z_{1:k-1})= \int P(T_k \vert T_{k-1},T_0,u_{1:k},z_{1:k-1})P(T_{k-1} \vert T_0,u_{1:k},z_{1:k-1})dT_{k-1} P ( T k ∣ T 0 , u 1 : k , z 1 : k − 1 ) = ∫ P ( T k ∣ T k − 1 , T 0 , u 1 : k , z 1 : k − 1 ) P ( T k − 1 ∣ T 0 , u 1 : k , z 1 : k − 1 ) d T k − 1
假设k k k k − 1 k-1 k − 1
P ( T k ∣ T 0 , u 1 : k , z 1 : k − 1 ) = ∫ P ( T k ∣ T k − 1 , u k ) P ( T k − 1 ∣ T 0 , u 1 : k − 1 , z 1 : k − 1 ) d T k − 1 P(T_k \vert T_0,u_{1:k},z_{1:k-1})= \int P(T_k \vert T_{k-1},u_k)P(T_{k-1} \vert T_0,u_{1:k-1},z_{1:k-1})dT_{k-1} P ( T k ∣ T 0 , u 1 : k , z 1 : k − 1 ) = ∫ P ( T k ∣ T k − 1 , u k ) P ( T k − 1 ∣ T 0 , u 1 : k − 1 , z 1 : k − 1 ) d T k − 1
上述第一项消去了k − 1 k-1 k − 1 u k u_k u k k k k u k u_k u k k − 1 k-1 k − 1
对比一下可以发现,左侧是k k k k − 1 k-1 k − 1
假设是一个线性系统,且噪声满足方差不变的正态分布,即:
T k = A k T k − 1 + u k + w k , w k ∼ N ( 0 , R ) T_k=A_k T_{k-1} + u_k+w_k \, , \, w_k \sim N(0,R) T k = A k T k − 1 + u k + w k , w k ∼ N ( 0 , R )
z k = C k T k + v k , v k ∼ N ( 0 , Q ) z_k=C_k T_k+v_k \, , \, v_k \sim N(0,Q) z k = C k T k + v k , v k ∼ N ( 0 , Q )
仅通过运动方程推出的称为先验,表示为T k ˉ \bar {T_k} T k ˉ
经过观测方程后得到的称为后验,表示为T k ^ \hat{T_k} T k ^
卡尔曼滤波要实现的就是:已知k − 1 k-1 k − 1 k k k k k k
① 从k − 1 k-1 k − 1 k k k
假设后验到真实值满足高斯分布:T k − 1 ∼ N ( T ^ k − 1 , ∑ ^ k − 1 ) T_{k-1} \sim N(\hat{T}_{k-1},\hat{\sum}_{k-1}) T k − 1 ∼ N ( T ^ k − 1 , ∑ ^ k − 1 ) ∑ \sum ∑
T ˉ k = A k T k − 1 + u k + w k = A k N ( T ^ k − 1 , ∑ ^ k − 1 ) + N ( u k , 0 ) + N ( 0 , R ) ∼ N ( A k T ^ k − 1 + u k , A k ∑ ^ k − 1 A k T + R ) \bar{T}_k = A_k T_{k-1} + u_k+w_k = A_k N(\hat{T}_{k-1},\hat{\sum}_{k-1})+N(u_k,0)+N(0,R) \sim N(A_k\hat{T}_{k-1}+u_k,A_k \hat{\sum}_{k-1}A_k^{T}+R) T ˉ k = A k T k − 1 + u k + w k = A k N ( T ^ k − 1 , ∑ ^ k − 1 ) + N ( u k , 0 ) + N ( 0 , R ) ∼ N ( A k T ^ k − 1 + u k , A k ∑ ^ k − 1 A k T + R )
这里涉及到知识,假设X ∼ N ( μ , σ 2 ) X \sim N(\mu,\sigma^2) X ∼ N ( μ , σ 2 ) a X + b ∼ N ( a μ + b , a 2 σ 2 ) aX+b \sim N(a\mu+b,a^2\sigma^2) a X + b ∼ N ( a μ + b , a 2 σ 2 )
所以k k k T ˉ k = A k T ^ k − 1 + u k , ∑ ˉ k = A k ∑ ^ k − 1 A k T + R \bar{T}_k = A_k\hat{T}_{k-1}+u_k \, , \, \bar{\sum}_{k} = A_k \hat{\sum}_{k-1}A_k^{T}+R T ˉ k = A k T ^ k − 1 + u k , ∑ ˉ k = A k ∑ ^ k − 1 A k T + R
② 从k k k k k k
由观测方程z k = C k T k + v k z_k=C_k T_k+v_k z k = C k T k + v k P ( z k ∣ T k ) = N ( C k T k , Q ) P(z_k \vert T_k) = N(C_kT_k,Q) P ( z k ∣ T k ) = N ( C k T k , Q )
对于上述推出的关系P ( T k ∣ T 0 , u 1 : k , z 1 : k ) ∝ P ( z k ∣ T k ) P ( T k ∣ T 0 , u 1 : k , z 1 : k − 1 ) P(T_k \vert T_0,u_{1:k},z_{1:k}) \propto P(z_k \vert T_k) P(T_k \vert T_0,u_{1:k},z_{1:k-1}) P ( T k ∣ T 0 , u 1 : k , z 1 : k ) ∝ P ( z k ∣ T k ) P ( T k ∣ T 0 , u 1 : k , z 1 : k − 1 )
N ( T ^ k , ∑ ^ k ) ∝ N ( C k T k , Q ) N ( T ˉ k , ∑ ˉ k ) N(\hat{T}_k,\hat{\sum}_{k}) \propto N(C_kT_k,Q) N(\bar{T}_k,\bar{\sum}_{k}) N ( T ^ k , ∑ ^ k ) ∝ N ( C k T k , Q ) N ( T ˉ k , ∑ ˉ k )
上述正比关系,式子两侧相差一个系数,两个正态分布相乘,结果是一个正态分布乘以一个系数,
而这两个系数不会影响到指数项,故从指数项下手求解
对于正态分布N ∼ ( μ 1 , σ 1 2 ) N \sim(\mu_1,\sigma_1^2) N ∼ ( μ 1 , σ 1 2 ) ( x − μ 1 ) 2 ( σ 1 2 ) − 1 (x-\mu_1)^2(\sigma_1^2)^{-1} ( x − μ 1 ) 2 ( σ 1 2 ) − 1
f ( x ) = 1 2 π σ 1 e − ( x − μ 1 ) 2 2 σ 1 2 = 1 2 π σ 1 e − 1 2 ( x − μ 1 ) 2 ( σ 1 2 ) − 1 f(x) =\frac{1}{\sqrt{2\pi}\sigma_1}e^{-\frac{(x-\mu_1)^2}{2\sigma_1^2} } = \frac{1}{\sqrt{2\pi}\sigma_1}e^{-\frac{1}{2}{(x-\mu_1)^2}{(\sigma_1^2)^{-1}} }
f ( x ) = 2 π σ 1 1 e − 2 σ 1 2 ( x − μ 1 ) 2 = 2 π σ 1 1 e − 2 1 ( x − μ 1 ) 2 ( σ 1 2 ) − 1
对于矩阵正态分布N ∼ ( X , ∑ ) N \sim (X,\sum) N ∼ ( X , ∑ ) ∑ \sum ∑ ( x − X ) T ∑ − 1 ( x − X ) (x-X)^T\sum^{-1}(x-X) ( x − X ) T ∑ − 1 ( x − X )
将上述代入可得:
( T k − T ^ k ) T ∑ ^ k − 1 ( T k − T ^ k ) = ( z k − C k T k ) T Q − 1 ( z k − C k T k ) + ( T k − T ˉ k ) T ∑ ˉ k − 1 ( T k − T ˉ k ) (T_k-\hat{T}_k)^T \hat{\sum}_{k}^{-1}(T_k-\hat{T}_k) = (z_k-C_k T_k)^T Q^{-1}(z_k-C_k T_k) + (T_k-\bar{T}_k)^T \bar{\sum}_{k}^{-1}(T_k-\bar{T}_k) ( T k − T ^ k ) T ∑ ^ k − 1 ( T k − T ^ k ) = ( z k − C k T k ) T Q − 1 ( z k − C k T k ) + ( T k − T ˉ k ) T ∑ ˉ k − 1 ( T k − T ˉ k )
对于T k T_k T k
∑ ^ k − 1 = C k T Q − 1 C k + ∑ ˉ k − 1 \hat{\sum}_{k}^{-1} = C_k^TQ^{-1}C_k+ \bar{\sum}_{k}^{-1} ∑ ^ k − 1 = C k T Q − 1 C k + ∑ ˉ k − 1
对于T k T_k T k
T ^ k T ∑ ^ k − 1 = z k T Q − 1 C k + T ˉ k T ∑ ˉ k − 1 \hat{T}_k^T\hat{\sum}_{k}^{-1} =z_k^TQ^{-1}C_k+ \bar{T}_k^T\bar{\sum}_{k}^{-1} T ^ k T ∑ ^ k − 1 = z k T Q − 1 C k + T ˉ k T ∑ ˉ k − 1
去转置得:
∑ ^ k − 1 T ^ k = C k T Q − 1 z k + ∑ ˉ k − 1 T ˉ k \hat{\sum}_{k}^{-1} \hat{T}_k = C_k^TQ^{-1}z_k+ \bar{\sum}_{k}^{-1} \bar{T}_k ∑ ^ k − 1 T ^ k = C k T Q − 1 z k + ∑ ˉ k − 1 T ˉ k
②式左右同时左乘∑ ^ k \hat{\sum}_{k} ∑ ^ k
T ^ k = ∑ ^ k C k T Q − 1 z k + ∑ ^ k ∑ ˉ k − 1 T ˉ k \hat{T}_k = \hat{\sum}_{k} C_k^TQ^{-1}z_k+ \hat{\sum}_{k} \bar{\sum}_{k}^{-1} \bar{T}_k T ^ k = ∑ ^ k C k T Q − 1 z k + ∑ ^ k ∑ ˉ k − 1 T ˉ k
定义K = ∑ ^ k C k T Q − 1 K=\hat{\sum}_{k} C_k^TQ^{-1} K = ∑ ^ k C k T Q − 1
T ^ k = K z k + ∑ ^ k ∑ ˉ k − 1 T ˉ k \hat{T}_k = K z_k+ \hat{\sum}_{k} \bar{\sum}_{k}^{-1} \bar{T}_k T ^ k = K z k + ∑ ^ k ∑ ˉ k − 1 T ˉ k
根据①消去∑ ˉ k − 1 \bar{\sum}_{k}^{-1} ∑ ˉ k − 1
T ^ k = K z k + ∑ ^ k ( ∑ ^ k − 1 − C k T Q − 1 C k ) T ˉ k = K z k + ( I − K C k ) T ˉ k = T ˉ k + K ( z k − C k T ˉ k ) \hat{T}_k = K z_k+ \hat{\sum}_{k} (\hat{\sum}_{k}^{-1} - C_k^TQ^{-1}C_k) \bar{T}_k = K z_k + (I-KC_k) \bar{T}_k = \bar{T}_k + K(z_k-C_k \bar{T}_k) T ^ k = K z k + ∑ ^ k ( ∑ ^ k − 1 − C k T Q − 1 C k ) T ˉ k = K z k + ( I − K C k ) T ˉ k = T ˉ k + K ( z k − C k T ˉ k )
算完T ^ k \hat{T}_k T ^ k ∑ ^ k \hat{\sum}_{k} ∑ ^ k
对于①式左右同时左乘∑ ^ k \hat{\sum}_{k} ∑ ^ k
I = ∑ ^ k C k T Q − 1 C k + ∑ ^ k ∑ ˉ k − 1 = K C k + ∑ ^ k ∑ ˉ k − 1 I = \hat{\sum}_{k} C_k^TQ^{-1}C_k+ \hat{\sum}_{k} \bar{\sum}_{k}^{-1} = KC_k + \hat{\sum}_{k} \bar{\sum}_{k}^{-1} I = ∑ ^ k C k T Q − 1 C k + ∑ ^ k ∑ ˉ k − 1 = K C k + ∑ ^ k ∑ ˉ k − 1
整理一下有∑ ^ k = ( I − K C k ) ∑ ˉ k \hat{\sum}_{k} =(I-KC_k)\bar{\sum}_{k} ∑ ^ k = ( I − K C k ) ∑ ˉ k
最后最后还要整理一下卡尔曼增益K K K
把∑ ^ k = ( I − K C k ) ∑ ˉ k \hat{\sum}_{k} =(I-KC_k)\bar{\sum}_{k} ∑ ^ k = ( I − K C k ) ∑ ˉ k K = ∑ ^ k C k T Q − 1 K=\hat{\sum}_{k} C_k^TQ^{-1} K = ∑ ^ k C k T Q − 1 K = ( ( I − K C k ) ∑ ˉ k ) C k T Q − 1 K = ((I-KC_k)\bar{\sum}_{k}) C_k^T Q^{-1} K = ( ( I − K C k ) ∑ ˉ k ) C k T Q − 1
右乘Q Q Q K Q = ( I − K C k ) ∑ ˉ k C k T K Q = (I-K C_k) \bar{ \sum }_{k} C_k^T K Q = ( I − K C k ) ∑ ˉ k C k T
把K K K K = ∑ ˉ k C k T ( C k ∑ ˉ k C k T + Q ) − 1 K = \bar{\sum}_{k} C_k^T {(C_k \bar{\sum}_{k} C_k^T + Q)}^{-1} K = ∑ ˉ k C k T ( C k ∑ ˉ k C k T + Q ) − 1
对于线性系统:
T k = A k T k − 1 + u k + w k , w k ∼ N ( 0 , R ) T_k=A_k T_{k-1} + u_k+w_k \, , \, w_k \sim N(0,R) T k = A k T k − 1 + u k + w k , w k ∼ N ( 0 , R )
z k = C k T k + v k , v k ∼ N ( 0 , Q ) z_k=C_k T_k+v_k \, , \, v_k \sim N(0,Q) z k = C k T k + v k , v k ∼ N ( 0 , Q )
后验到真实值满足高斯分布:T k − 1 ∼ N ( T ^ k − 1 , ∑ ^ k − 1 ) T_{k-1} \sim N(\hat{T}_{k-1},\hat{\sum}_{k-1}) T k − 1 ∼ N ( T ^ k − 1 , ∑ ^ k − 1 )
预测:
T ˉ k = A k T ^ k − 1 + u k \bar{T}_k = A_k\hat{T}_{k-1}+u_k T ˉ k = A k T ^ k − 1 + u k
∑ ˉ k = A k ∑ ^ k − 1 A k T + R \bar{\sum}_k = A_k \hat{\sum}_{k-1} A_k^{T}+R ∑ ˉ k = A k ∑ ^ k − 1 A k T + R
更新:
K = ∑ ˉ k C k T ( C k ∑ ˉ k C k T + Q ) − 1 K = \bar{\sum}_{k} C_k^T {(C_k \bar{\sum}_{k} C_k^T + Q)}^{-1} K = ∑ ˉ k C k T ( C k ∑ ˉ k C k T + Q ) − 1
T ^ k = T ˉ k + K ( z k − C k T ˉ k ) \hat{T}_k = \bar{T}_k + K(z_k-C_k \bar{T}_k) T ^ k = T ˉ k + K ( z k − C k T ˉ k )
∑ ^ k = ( I − K C k ) ∑ ˉ k \hat{\sum}_{k} =(I-KC_k)\bar{\sum}_{k} ∑ ^ k = ( I − K C k ) ∑ ˉ k
对于非线性系统
T k = f ( T k − 1 , u k ) + w k T_k = f(T_{k-1},u_k)+w_k T k = f ( T k − 1 , u k ) + w k
z k = h ( T k ) + v k z_k = h(T_k)+v_k z k = h ( T k ) + v k
一般将运动方程和观测方程在工作点附近进行一阶泰勒展开,近似线性,即:
T k ≈ f ( T ^ k − 1 , u k ) + ∂ f ∂ T k − 1 ∣ T ^ k − 1 ( T k − 1 − T ^ k − 1 ) + w k = f ( T ^ k − 1 , u k ) + F ( T k − 1 − T ^ k − 1 ) + w k T_k \approx f(\hat{T}_{k-1},u_k)+ \frac{\partial f}{\partial T_{k-1}} |_{\hat{T}_{k-1}} (T_{k-1} - \hat{T}_{k-1}) + w_k = f(\hat{T}_{k-1},u_k)+ F (T_{k-1} - \hat{T}_{k-1}) + w_k T k ≈ f ( T ^ k − 1 , u k ) + ∂ T k − 1 ∂ f ∣ T ^ k − 1 ( T k − 1 − T ^ k − 1 ) + w k = f ( T ^ k − 1 , u k ) + F ( T k − 1 − T ^ k − 1 ) + w k
z k ≈ h ( T ˉ k ) + ∂ h ∂ T k ∣ T ˉ k ( T k − T ˉ k ) + v k = h ( T ˉ k ) + H ( T k − T ˉ k ) + v k z_k \approx h(\bar{T}_k)+\frac{\partial h}{\partial T_k} |_{\bar{T}_k} (T_k - \bar{T}_k) +v_k = h(\bar{T}_k)+H(T_k - \bar{T}_k) +v_k z k ≈ h ( T ˉ k ) + ∂ T k ∂ h ∣ T ˉ k ( T k − T ˉ k ) + v k = h ( T ˉ k ) + H ( T k − T ˉ k ) + v k
同理可推导
预测:
T ˉ k = f ( T ^ k − 1 , u k ) \bar{T}_{k} = f( \hat{T}_{k-1}, u_k) T ˉ k = f ( T ^ k − 1 , u k )
∑ ˉ k = F ∑ ^ k − 1 F T + R \bar{\sum}_k = F \hat{\sum}_{k-1} F^{T}+R ∑ ˉ k = F ∑ ^ k − 1 F T + R
更新:
K = ∑ ˉ k H T ( H ∑ ˉ k H T + Q ) − 1 K = \bar{\sum}_{k} H^T {(H \bar{\sum}_{k} H^T + Q)}^{-1} K = ∑ ˉ k H T ( H ∑ ˉ k H T + Q ) − 1
T ^ k = T ˉ k + K ( z k − h ( T ˉ k ) ) \hat{T}_k = \bar{T}_k + K(z_k-h(\bar{T}_k) ) T ^ k = T ˉ k + K ( z k − h ( T ˉ k ) )
∑ ^ k = ( I − K H ) ∑ ˉ k \hat{\sum}_{k} =(I-KH)\bar{\sum}_{k} ∑ ^ k = ( I − K H ) ∑ ˉ k
优点:适用性强,常用于多传感器融合
缺点:一阶马尔可夫性过于简单、数据有离散点可能会发散
目前视觉SLAM 主流为非线性优化方法,不假设马尔可夫性,即考虑 k k k
假设世界坐标系下一点p p p P ′ = R p + t = [ X ′ , Y ′ , Z ′ ] T P'=Rp+t = [X',Y',Z']^T P ′ = R p + t = [ X ′ , Y ′ , Z ′ ] T
将P ′ P' P ′ P c = [ u c , v c , 1 ] T = [ X ′ Z ′ , Y ′ Z ′ , 1 ] T P_c =[u_c,v_c,1]^T = [\frac{X'}{Z'},\frac{Y'}{Z'},1]^T P c = [ u c , v c , 1 ] T = [ Z ′ X ′ , Z ′ Y ′ , 1 ] T
去径向畸变得,u c ′ = u c ( 1 + k 1 r c 2 + k 2 r c 4 ) , v c ′ = v c ( 1 + k 1 r c 2 + k 2 r c 4 ) , r c 2 = u c 2 + v c 2 u_c'=u_c(1+k_1 r_c^2+k_2 r_c^4) \, , \, v_c'=v_c(1+k_1 r_c^2+k_2 r_c^4) \, , \, r_c^2 =u_c^2 +v_c^2 u c ′ = u c ( 1 + k 1 r c 2 + k 2 r c 4 ) , v c ′ = v c ( 1 + k 1 r c 2 + k 2 r c 4 ) , r c 2 = u c 2 + v c 2
通过内参计算像素得,u s = f x u c ′ + c x , v s = f y v c ′ + c y u_s = f_x u_c'+c_x \, , \, v_s =f_y v_c'+c_y u s = f x u c ′ + c x , v s = f y v c ′ + c y
上述过程其实就是由世界坐标p p p [ u s , x s ] T [u_s,x_s]^T [ u s , x s ] T z = [ u s , v s ] T = h ( ξ , p ) z = [u_s,v_s]^T = h(\xi,p) z = [ u s , v s ] T = h ( ξ , p ) ξ \xi ξ R , t R,t R , t
故我们可以定义误差S = 1 2 ∑ i ∑ j ∣ ∣ z i j − h ( ξ i , p j ) ∣ ∣ T S = \frac{1}{2}\sum_{i}\sum_{j} {\vert\vert z_{ij}-h(\xi_i,p_j)\vert\vert}^T S = 2 1 ∑ i ∑ j ∣ ∣ z i j − h ( ξ i , p j ) ∣ ∣ T
将待优化的量定义在一起x = [ ξ 1 , . . . , ξ m , p i , . . . , p n ] T x = [\xi_1,...,\xi_m,p_i,...,p_n]^T x = [ ξ 1 , . . . , ξ m , p i , . . . , p n ] T
给自变量一个增量,1 2 ∣ ∣ f ( x + Δ x ) ∣ ∣ T ≈ 1 2 ∑ i ∑ j ∣ ∣ z i j − h ( ξ i , p j ) + F i j Δ ξ i + E i j Δ p j ∣ ∣ T \frac{1}{2} {\vert\vert f(x+\Delta x) \vert\vert}^T \approx \frac{1}{2}\sum_{i}\sum_{j} {\vert\vert z_{ij}-h(\xi_i,p_j) +F_{ij}\Delta \xi_i +E_{ij}\Delta p_j \vert\vert}^T 2 1 ∣ ∣ f ( x + Δ x ) ∣ ∣ T ≈ 2 1 ∑ i ∑ j ∣ ∣ z i j − h ( ξ i , p j ) + F i j Δ ξ i + E i j Δ p j ∣ ∣ T
其中F i j F_{ij} F i j F i j = ∂ e ∂ δ ξ = − [ f x Z ′ 0 − f x X ′ Z ′ 2 − f x X ′ Y ′ Z ′ 2 f x + f x X ′ 2 Z ′ 2 − f x Y ′ Z ′ 0 f y Z ′ − f y Y ′ Z ′ 2 − f y − f y Y ′ 2 Z ′ 2 f y X ′ Y ′ Z ′ 2 f y X ′ Z ′ ] F_{ij} = \frac{\partial e}{\partial \delta \xi} = -\begin{bmatrix} \frac{f_x}{Z'}&0&-\frac{f_xX'}{Z'^2}&-\frac{f_xX'Y'}{Z'^2}&f_x+\frac{f_xX'^2}{Z'^2}&-\frac{f_xY'}{Z'} \\ 0&\frac{f_y}{Z'}&-\frac{f_yY'}{Z'^2}&-f_y-\frac{f_yY'^2}{Z'^2}&\frac{f_yX'Y'}{Z'^2}&\frac{f_yX'}{Z'}\end{bmatrix} F i j = ∂ δ ξ ∂ e = − [ Z ′ f x 0 0 Z ′ f y − Z ′ 2 f x X ′ − Z ′ 2 f y Y ′ − Z ′ 2 f x X ′ Y ′ − f y − Z ′ 2 f y Y ′ 2 f x + Z ′ 2 f x X ′ 2 Z ′ 2 f y X ′ Y ′ − Z ′ f x Y ′ Z ′ f y X ′ ]
E i j E_{ij} E i j E i j = ∂ e ∂ P = − [ f x Z ′ 0 − f x X ′ Z ′ 2 0 f y Z ′ − f y Y ′ Z ′ 2 ] R E_{ij}=\frac{\partial e}{\partial P}= -\begin{bmatrix} \frac{f_x}{Z'} & 0 & -\frac{f_x X'}{Z'^2} \\ 0 & \frac{f_y}{Z'} &-\frac{f_y Y'}{Z'^2} \end{bmatrix} R E i j = ∂ P ∂ e = − [ Z ′ f x 0 0 Z ′ f y − Z ′ 2 f x X ′ − Z ′ 2 f y Y ′ ] R
为了把式子写得更整体而不是各项和,将位姿放在一起x c = [ ξ 1 , ξ 2 , . . . , ξ m ] T ∈ R 6 m × 1 x_c=[\xi_1,\xi_2,...,\xi_m]^T \in R^{6m \times 1} x c = [ ξ 1 , ξ 2 , . . . , ξ m ] T ∈ R 6 m × 1 x p = [ p 1 , p 2 , . . . , p n ] T ∈ R 3 n × 1 x_p =[p_1,p_2,...,p_n]^T \in R^{3n \times 1} x p = [ p 1 , p 2 , . . . , p n ] T ∈ R 3 n × 1
则有,1 2 ∣ ∣ f ( x + Δ x ) ∣ ∣ T = 1 2 ∣ ∣ e + F Δ x c + E Δ x p ∣ ∣ T \frac{1}{2} {\vert\vert f(x+\Delta x) \vert\vert}^T = \frac{1}{2}{\vert\vert e +F\Delta x_c +E\Delta x_p \vert\vert}^T 2 1 ∣ ∣ f ( x + Δ x ) ∣ ∣ T = 2 1 ∣ ∣ e + F Δ x c + E Δ x p ∣ ∣ T F = [ F 1 , F 2 , . . . , F m ] ∈ R 2 × 6 m , E = [ E 1 . E 2 , . . . , E n ] ∈ R 2 × 3 n F=[F_1,F_2,...,F_m] \in R^{2 \times 6m}, E = [E_1.E_2,...,E_n] \in R^{2 \times 3n} F = [ F 1 , F 2 , . . . , F m ] ∈ R 2 × 6 m , E = [ E 1 . E 2 , . . . , E n ] ∈ R 2 × 3 n
求解非线性最小二乘,最终都会要计算增量方程H Δ x = g H \Delta x = g H Δ x = g
对于GN法,J T ( x ) J ( x ) Δ x = g J^T(x)J(x)\Delta x = g J T ( x ) J ( x ) Δ x = g
其中J = [ F E ] ∈ R 2 × ( 6 m + 3 n ) , J T = [ F T E T ] ∈ R ( 6 m + 3 n ) × 2 , H = J T J = [ F T F F T E E T F E T E ] ∈ R ( 6 m + 3 n ) × ( 6 m + 3 n ) J =\begin{bmatrix}F&E \end{bmatrix} \in R^{2 \times(6m+3n)},J^T= \begin{bmatrix}F^T \\E^T \end{bmatrix} \in R^{(6m+3n) \times 2}, H = J^TJ=\begin{bmatrix}F^TF & F^TE \\ E^T F& E^TE \end{bmatrix} \in R^{(6m+3n) \times (6m+3n)} J = [ F E ] ∈ R 2 × ( 6 m + 3 n ) , J T = [ F T E T ] ∈ R ( 6 m + 3 n ) × 2 , H = J T J = [ F T F E T F F T E E T E ] ∈ R ( 6 m + 3 n ) × ( 6 m + 3 n )
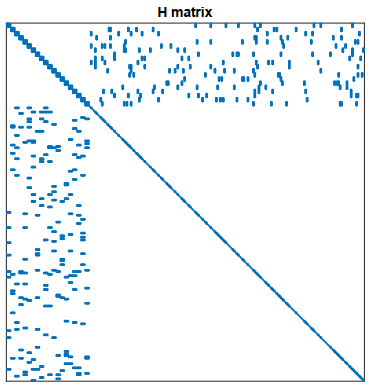
由于路标点数量n n n H H H
由于H H H
稀疏,简单来讲就是矩阵里有很多元素是0,
H H H J ( x ) J(x) J ( x )
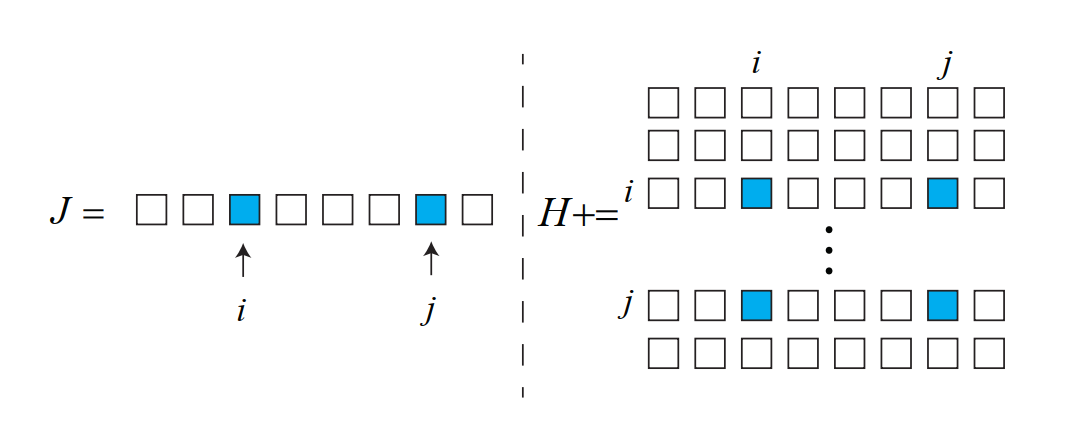
J i j ( x ) = ( 0 2 × 6 , . . . 0 2 × 6 , ∂ e i j ∂ ξ i , . . . 0 2 × 6 , 0 2 × 6 , 0 2 × 3 , . . . 0 2 × 3 , ∂ e i j ∂ p j , . . . 0 2 × 3 , 0 2 × 3 ) J_{ij}(x)=(0_{2\times6},...0_{2\times6},\frac{\partial e_{ij}}{\partial \xi_i},...0_{2\times6},0_{2\times6},0_{2\times3},...0_{2\times3},\frac{\partial e_{ij}}{\partial p_j},...0_{2\times3},0_{2\times3}) J i j ( x ) = ( 0 2 × 6 , . . . 0 2 × 6 , ∂ ξ i ∂ e i j , . . . 0 2 × 6 , 0 2 × 6 , 0 2 × 3 , . . . 0 2 × 3 , ∂ p j ∂ e i j , . . . 0 2 × 3 , 0 2 × 3 )
在位姿ξ i \xi_i ξ i p j p_j p j i , j i,j i , j H H H
对于整体的H H H H = ∑ i , j J i j T J i j H=\sum_{i,j}J_{ij}^TJ_{ij} H = ∑ i , j J i j T J i j
某个位姿观测到了某个路标点,对应H H H
H H H
我们可以对其Schur消元,在SLAM研究中也称为Marginalization(边缘化)
我们假设H = [ B E E T C ] H = \begin{bmatrix}B&E \\ E^T & C \end{bmatrix} H = [ B E T E C ] B B B C C C B B B C C C
则H Δ x = g H \Delta x = g H Δ x = g [ B E E T C ] [ Δ x c Δ x p ] = [ v w ] \begin{bmatrix}B&E \\ E^T & C \end{bmatrix} \begin{bmatrix} \Delta x_c \\ \Delta x_p\end{bmatrix} = \begin{bmatrix} v \\ w\end{bmatrix} [ B E T E C ] [ Δ x c Δ x p ] = [ v w ]
高斯消元[ I − E C − 1 0 I ] [ B E E T C ] [ Δ x c Δ x p ] = [ I − E C − 1 0 I ] [ v w ] \begin{bmatrix}I&-EC^{-1} \\ 0 & I \end{bmatrix} \begin{bmatrix}B&E \\ E^T & C \end{bmatrix} \begin{bmatrix} \Delta x_c \\ \Delta x_p\end{bmatrix} = \begin{bmatrix}I&-EC^{-1} \\ 0 & I \end{bmatrix}\begin{bmatrix} v \\ w\end{bmatrix} [ I 0 − E C − 1 I ] [ B E T E C ] [ Δ x c Δ x p ] = [ I 0 − E C − 1 I ] [ v w ]
化简得[ B − E C − 1 E T 0 E T C ] [ Δ x c Δ x p ] = [ v − E C − 1 w w ] \begin{bmatrix}B-EC^{-1}E^T & 0 \\ E^T & C \end{bmatrix} \begin{bmatrix} \Delta x_c \\ \Delta x_p\end{bmatrix} = \begin{bmatrix} v-EC^{-1}w \\ w\end{bmatrix} [ B − E C − 1 E T E T 0 C ] [ Δ x c Δ x p ] = [ v − E C − 1 w w ]
这样第一行方程组就与Δ x p \Delta x_p Δ x p [ B − E C − 1 E T ] Δ x c = v − E C − 1 w [B-EC^{-1}E^T]\Delta x_c = v-EC^{-1}w [ B − E C − 1 E T ] Δ x c = v − E C − 1 w
我们可以先通过这个方程组解出Δ x c \Delta x_c Δ x c E T Δ x c + C Δ x p = w E^T \Delta x_c + C \Delta x_p =w E T Δ x c + C Δ x p = w Δ x p \Delta x_p Δ x p
因为路标点的维度比较大,这样做可以加速求解,而且C C C
从概率的角度来讲,我们实际上把求 ( Δ x c , Δ x p ) (\Delta x_c,\Delta x_p) ( Δ x c , Δ x p ) Δ x c \Delta x_c Δ x c Δ x p \Delta x_p Δ x p
相当于进行了条件概率展开P ( x c , x p ) = P ( x c ) P ( x p ∣ x c ) P(x_c,x_p)=P(x_c)P(x_p\vert x_c) P ( x c , x p ) = P ( x c ) P ( x p ∣ x c ) x c x_c x c
为了避免某个误差项导致整个优化朝错误的方向进行,可以采用核函数
核函数可以保证优化的每条边的误差不会太大以掩盖掉其他的边
具体的做法是把原先误差的二范数度量,替换成一个增长较慢的函数,同时自身又要光滑可导
以常用的Huber核为例
H ( e ) = { 1 2 e 2 , ∣ e ∣ ≤ δ δ ( ∣ e ∣ − 1 2 δ ) , o t h e r w i s e H(e) =\left\{\begin{matrix} \frac{1}{2}e^2,&\vert e \vert \le \delta \\ \delta(\vert e\vert -\frac{1}{2}\delta),&otherwise\end{matrix}\right. H ( e ) = { 2 1 e 2 , δ ( ∣ e ∣ − 2 1 δ ) , ∣ e ∣ ≤ δ o t h e r w i s e
实际上就是将误差太大时的二次增长改成一次增长
直接命令行安装即可
sudo apt-get install meshlab
打开时颜色会比较暗,在右侧把shading改成None就可以了
数据集:https://grail.cs.washington.edu/projects/bal/index.html
全局图优化有个缺点,就是机器人运行的越久,地图越来越大
全局图优化会非常耗时,而这其中占主要部分的是特征点优化
但经过若干次观测之后,收敛的特征点的空间位置估计就会收敛至一个值保持不动
花费大量计算资源计算再对这些特征点进行优化是不明智的,
所以一般在优化几次之后就把特征点固定住,只对位姿进行优化
在Pose Graph图优化中
节点是相机位姿,我们表示为ξ 1 , ξ 2 , . . . , ξ n \xi_1,\xi_2,...,\xi_n ξ 1 , ξ 2 , . . . , ξ n
边是两个位姿节点之间相对运动的估计,记ξ i \xi_i ξ i ξ j \xi_j ξ j Δ ξ i j \Delta \xi_{ij} Δ ξ i j
按照李群的写法为:Δ T i j = T i − 1 T j \Delta T_{ij}=T_i^{-1}T_j Δ T i j = T i − 1 T j Δ ξ i j = l n ( e x p ( ( − ξ i ) ^ ) e x p ( ξ j ^ ) ) ˇ \Delta \xi_{ij} =ln(exp((-\xi_i)\hat{})exp(\xi_j\hat{}))\check{} Δ ξ i j = l n ( e x p ( ( − ξ i ) ^ ) e x p ( ξ j ^ ) ) ˇ
把Δ T i j \Delta T_{ij} Δ T i j e i j = l n ( Δ T i j − 1 T i − 1 T j ) ˇ = l n ( e x p ( ( − ξ i j ) ^ ) e x p ( ( − ξ i ) ^ ) e x p ( ξ j ^ ) ) ˇ e_{ij} = ln(\Delta T_{ij}^{-1}T_i^{-1}T_j)\check{} = ln(exp((-\xi_{ij})\hat{})exp((-\xi_{i})\hat{})exp(\xi_j\hat{}))\check{} e i j = l n ( Δ T i j − 1 T i − 1 T j ) ˇ = l n ( e x p ( ( − ξ i j ) ^ ) e x p ( ( − ξ i ) ^ ) e x p ( ξ j ^ ) ) ˇ
给ξ i \xi_i ξ i ξ j \xi_j ξ j δ ξ i \delta\xi_i δ ξ i δ ξ j \delta\xi_j δ ξ j e i j ^ = l n ( T i j − 1 T i − 1 e x p ( ( − δ ξ i ) ^ ) e x p ( δ ξ j ^ ) T j ) ˇ \hat{e_{ij}} = ln(T_{ij}^{-1}T_i^{-1}exp((-\delta\xi_i)\hat{})exp(\delta\xi_j\hat{})T_j)\check{} e i j ^ = l n ( T i j − 1 T i − 1 e x p ( ( − δ ξ i ) ^ ) e x p ( δ ξ j ^ ) T j ) ˇ
为了将扰动项移到右侧(或左侧),需要用到伴随性质:T e x p ( ξ ^ ) T − 1 = e x p ( ( A d ( T ) ξ ) ^ ) , A d ( T ) = [ R t ^ 0 R ] Texp(\xi\hat{})T^{-1}=exp((Ad(T)\xi)\hat{}) \,\, ,\,\,Ad(T)=\begin{bmatrix}R & t\hat{} \\ 0 & R \end{bmatrix} T e x p ( ξ ^ ) T − 1 = e x p ( ( A d ( T ) ξ ) ^ ) , A d ( T ) = [ R 0 t ^ R ]
将T T T T − 1 T^{-1} T − 1 T − 1 e x p ( ξ ^ ) T = e x p ( ( A d ( T − 1 ) ξ ) ^ ) T^{-1}exp(\xi\hat{})T=exp((Ad(T^{-1})\xi)\hat{}) T − 1 e x p ( ξ ^ ) T = e x p ( ( A d ( T − 1 ) ξ ) ^ ) T T T e x p ( ξ ^ ) T = T e x p ( ( A d ( T − 1 ) ξ ) ^ ) exp(\xi\hat{})T=Texp((Ad(T^{-1})\xi)\hat{}) e x p ( ξ ^ ) T = T e x p ( ( A d ( T − 1 ) ξ ) ^ )
所以我们可以通过上式实现T T T e x p exp e x p
利用上式子,可以将扰动项移至最右
e i j ^ = l n ( T i j − 1 T i − 1 e x p ( ( − δ ξ i ) ^ ) e x p ( δ ξ j ^ ) T j ) ˇ = l n ( T i j − 1 T i − 1 e x p ( ( − δ ξ i ) ^ ) T j e x p ( ( A d ( T j − 1 ) δ ξ j ) ^ ) ) ˇ = l n ( T i j − 1 T i − 1 T j e x p ( ( A d ( T j − 1 ) ( − δ ξ i ) ) ^ ) e x p ( ( A d ( T j − 1 ) δ ξ j ) ^ ) ) ˇ \hat{e_{ij}} = ln(T_{ij}^{-1}T_i^{-1}exp((-\delta\xi_i)\hat{})exp(\delta\xi_j\hat{})T_j)\check{} \\
=ln(T_{ij}^{-1}T_i^{-1}exp((-\delta\xi_i)\hat{})T_jexp((Ad(T_j^{-1})\delta\xi_j)\hat{}))\check{} \\
=ln(T_{ij}^{-1}T_i^{-1}T_jexp((Ad(T_j^{-1})(-\delta\xi_i))\hat{})exp((Ad(T_j^{-1})\delta\xi_j)\hat{}))\check{}
e i j ^ = l n ( T i j − 1 T i − 1 e x p ( ( − δ ξ i ) ^ ) e x p ( δ ξ j ^ ) T j ) ˇ = l n ( T i j − 1 T i − 1 e x p ( ( − δ ξ i ) ^ ) T j e x p ( ( A d ( T j − 1 ) δ ξ j ) ^ ) ) ˇ = l n ( T i j − 1 T i − 1 T j e x p ( ( A d ( T j − 1 ) ( − δ ξ i ) ) ^ ) e x p ( ( A d ( T j − 1 ) δ ξ j ) ^ ) ) ˇ
利用BCH近似e x p ( ξ ^ ) e x p ( Δ ξ ^ ) ≈ e x p ( ( J r − 1 Δ ξ + ξ ) ^ ) exp(\xi\hat{})exp(\Delta\xi\hat{}) \approx exp((\mathcal{J}_r^{-1}\Delta\xi+\xi)\hat{}) e x p ( ξ ^ ) e x p ( Δ ξ ^ ) ≈ e x p ( ( J r − 1 Δ ξ + ξ ) ^ )
e i j ^ = l n ( T i j − 1 T i − 1 T j e x p ( ( A d ( T j − 1 ) ( − δ ξ i ) ) ^ ) e x p ( ( A d ( T j − 1 ) δ ξ j ) ^ ) ) ˇ = l n ( T i j − 1 T i − 1 e x p ( ξ j ^ ) e x p ( ( A d ( T j − 1 ) ( − δ ξ i ) ) ^ ) e x p ( ( A d ( T j − 1 ) δ ξ j ) ^ ) ) ˇ ≈ l n ( T i j − 1 T i − 1 e x p ( ( − J r − 1 A d ( T j − 1 ) δ ξ i + ξ j ) ^ ) e x p ( ( A d ( T j − 1 ) δ ξ j ) ^ ) ) ˇ ≈ l n ( T i j − 1 T i − 1 e x p ( J r − 1 A d ( T j − 1 ) δ ξ j − J r − 1 A d ( T j − 1 ) δ ξ i + ξ j ) ) ˇ = l n ( e x p ( − ξ i j ^ ) e x p ( − ξ i ^ ) e x p ( J r − 1 A d ( T j − 1 ) δ ξ j − J r − 1 A d ( T j − 1 ) δ ξ i + ξ j ) ) ˇ \hat{e_{ij}}
= ln(T_{ij}^{-1}T_i^{-1}T_jexp((Ad(T_j^{-1})(-\delta\xi_i))\hat{})exp((Ad(T_j^{-1})\delta\xi_j)\hat{}))\check{} \\
= ln(T_{ij}^{-1}T_i^{-1}exp(\xi_j\hat{})exp((Ad(T_j^{-1})(-\delta\xi_i))\hat{})exp((Ad(T_j^{-1})\delta\xi_j)\hat{}))\check{} \\
\approx ln(T_{ij}^{-1}T_i^{-1}exp((-\mathcal{J}_r^{-1}Ad(T_j^{-1})\delta\xi_i+\xi_j)\hat{})exp((Ad(T_j^{-1})\delta\xi_j)\hat{}))\check{} \\
\approx ln(T_{ij}^{-1}T_i^{-1}exp(\mathcal{J}_r^{-1}Ad(T_j^{-1})\delta\xi_j-\mathcal{J}_r^{-1}Ad(T_j^{-1})\delta\xi_i+\xi_j))\check{} \\
=ln(exp(-\xi_{ij}\hat{})exp(-\xi_i\hat{})exp(\mathcal{J}_r^{-1}Ad(T_j^{-1})\delta\xi_j-\mathcal{J}_r^{-1}Ad(T_j^{-1})\delta\xi_i+\xi_j))\check{}
e i j ^ = l n ( T i j − 1 T i − 1 T j e x p ( ( A d ( T j − 1 ) ( − δ ξ i ) ) ^ ) e x p ( ( A d ( T j − 1 ) δ ξ j ) ^ ) ) ˇ = l n ( T i j − 1 T i − 1 e x p ( ξ j ^ ) e x p ( ( A d ( T j − 1 ) ( − δ ξ i ) ) ^ ) e x p ( ( A d ( T j − 1 ) δ ξ j ) ^ ) ) ˇ ≈ l n ( T i j − 1 T i − 1 e x p ( ( − J r − 1 A d ( T j − 1 ) δ ξ i + ξ j ) ^ ) e x p ( ( A d ( T j − 1 ) δ ξ j ) ^ ) ) ˇ ≈ l n ( T i j − 1 T i − 1 e x p ( J r − 1 A d ( T j − 1 ) δ ξ j − J r − 1 A d ( T j − 1 ) δ ξ i + ξ j ) ) ˇ = l n ( e x p ( − ξ i j ^ ) e x p ( − ξ i ^ ) e x p ( J r − 1 A d ( T j − 1 ) δ ξ j − J r − 1 A d ( T j − 1 ) δ ξ i + ξ j ) ) ˇ
通过BCH近似l n ( e x p ( A ) e x p ( B ) ) = A + B + 1 2 [ A , B ] + 1 12 [ A , [ A , B ] ] − 1 12 [ B , [ A , B ] ] + . . . ≈ A + B ln(exp(A)exp(B)) = A + B +\frac{1}{2}[A,B]+\frac{1}{12}[A,[A,B]]-\frac{1}{12}[B,[A,B]]+... \approx A + B l n ( e x p ( A ) e x p ( B ) ) = A + B + 2 1 [ A , B ] + 1 2 1 [ A , [ A , B ] ] − 1 2 1 [ B , [ A , B ] ] + . . . ≈ A + B
e i j ^ ≈ l n ( e x p ( − ξ i j ^ ) e x p ( − ξ i ^ ) e x p ( J r − 1 A d ( T j − 1 ) δ ξ j − J r − 1 A d ( T j − 1 ) δ ξ i + ξ j ) ) ˇ ≈ l n ( e x p ( ξ j − ξ i j − ξ i − J r − 1 A d ( T j − 1 ) δ ξ i + J r − 1 A d ( T j − 1 ) δ ξ j ) ^ ) ˇ = ξ j − ξ i j − ξ i − J r − 1 A d ( T j − 1 ) δ ξ i + J r − 1 A d ( T j − 1 ) δ ξ j = e i j − J r − 1 A d ( T j − 1 ) δ ξ i + J r − 1 A d ( T j − 1 ) δ ξ j \hat{e_{ij}}
\approx ln(exp(-\xi_{ij}\hat{})exp(-\xi_i\hat{})exp(\mathcal{J}_r^{-1}Ad(T_j^{-1})\delta\xi_j-\mathcal{J}_r^{-1}Ad(T_j^{-1})\delta\xi_i+\xi_j))\check{} \\
\approx ln(exp(\xi_j-\xi_{ij}-\xi_i-\mathcal{J}_r^{-1}Ad(T_j^{-1})\delta\xi_i+\mathcal{J}_r^{-1}Ad(T_j^{-1})\delta\xi_j)\hat{})\check{} \\
= \xi_j-\xi_{ij}-\xi_i-\mathcal{J}_r^{-1}Ad(T_j^{-1})\delta\xi_i+\mathcal{J}_r^{-1}Ad(T_j^{-1})\delta\xi_j \\
=e_{ij}-\mathcal{J}_r^{-1}Ad(T_j^{-1})\delta\xi_i+\mathcal{J}_r^{-1}Ad(T_j^{-1})\delta\xi_j
e i j ^ ≈ l n ( e x p ( − ξ i j ^ ) e x p ( − ξ i ^ ) e x p ( J r − 1 A d ( T j − 1 ) δ ξ j − J r − 1 A d ( T j − 1 ) δ ξ i + ξ j ) ) ˇ ≈ l n ( e x p ( ξ j − ξ i j − ξ i − J r − 1 A d ( T j − 1 ) δ ξ i + J r − 1 A d ( T j − 1 ) δ ξ j ) ^ ) ˇ = ξ j − ξ i j − ξ i − J r − 1 A d ( T j − 1 ) δ ξ i + J r − 1 A d ( T j − 1 ) δ ξ j = e i j − J r − 1 A d ( T j − 1 ) δ ξ i + J r − 1 A d ( T j − 1 ) δ ξ j
其中J r − 1 ( e i j ) ≈ I + 1 2 [ ϕ e ^ ρ e ^ 0 ϕ e ^ ] \mathcal{J}_r^{-1}(e_{ij}) \approx I + \frac{1}{2}\begin{bmatrix}\hat{\phi_e} & \hat{\rho_e} \\ 0 & \hat{\phi_e}\end{bmatrix} J r − 1 ( e i j ) ≈ I + 2 1 [ ϕ e ^ 0 ρ e ^ ϕ e ^ ]
记ε \varepsilon ε T = min ξ 1 2 ∑ i , j ∈ ε ( e i , j T ∑ i j − 1 e i j ) T=\min_{\xi}\frac{1}{2}\sum_{i,j \in \varepsilon}(e_{i,j}^T\sum_{ij}^{-1}e_{ij}) T = min ξ 2 1 ∑ i , j ∈ ε ( e i , j T ∑ i j − 1 e i j )
可以看到在g2o/g2o/apps下是有g2o_viewer的,但是没有可执行文件
原因是缺失依赖,g2o_viewer没有编译
参考官方README:https://github.com/RainerKuemmerle/g2o
# 安装依赖
sudo apt-get install libsuitesparse-dev
sudo apt-get install qtdeclarative5-dev
sudo apt-get install qt5-qmake
sudo apt-get install libqglviewer-dev-qt5
# 重新编译
cd ~/g2o/build
cmake ..
make
sudo make install
sudo ldconfig
# 动态库链接更新
sudo ldconfig
参考:https://blog.csdn.net/weixin_42099090/article/details/106907271
参考:https://blog.csdn.net/u012348774/article/details/84144084
代码参考:https://github.com/qqqGpe/slam14-ch10-ceres
官网文档:http://ceres-solver.org
顶点:
VERTEX_SE3:QUAT index px py pz qx qy qz qw
边:
EDGE_SE3:QUAT idfrom idto px py pz qx qy qz qw 信息矩阵上三角
前端会产生累积误差,而后端采用位姿图优化,会导致优化轨迹产生偏移,
回环检测不止关注相邻帧,可以给出一些时隔更久的约束,可以用于消除累积误差,保证全局一致
正确的回环检测可以保证轨迹和地图在长时间下的正确性,就算跟踪算法丢失也可以用于重定位
在某些时候,我们把只有前端和局部后端的系统称为VO,而把带有回环检测和全局后端的系统称为SLAM
回环可以形象的理解为经过了同个(相似的)地方,从某个地方出发后又回到这个地方
我们需要预计哪一个地方可能出现回环,大体为两种思路:基于几何和基于外观
基于几何,简单来讲就是看里程计的值判断是否回到之前的某个位置,但是里程计又存在累积误差,没法用于准确判断
基于外观,简单来讲就是看两个图像的相似性,摆脱了累积误差,成为视觉SLAM中的主流做法
评价检测算法的好坏,书中引出了两个概念:感知偏差和感知变异
感知偏差对应假阳(FP),程序认为是回环,实际上不是回环
感知变异对应假阴(FN),程序认为不是回环,实际上是回环
准确率表示程序认为 是回环的所有中事实上 是回环的概率:P r e c i s i o n = T P T P + F P Precision=\frac{TP}{TP+FP} P r e c i s i o n = T P + F P T P
召回率表示事实上 是回环的所有中程序认为 是回环的概率:R e c a l l = T P T P + F N Recall=\frac{TP}{TP+FN} R e c a l l = T P + F N T P
这两者往往存在矛盾,但好的算法在高召回率下也能保持高准确率
条件放严时,检测到的回环少,召回率降低,但是准确率一般会提高
条件放松时,检测到的回环多,召回率升高,但是准确率一般会降低
在SLAM中,我们对准确率要求较为严格,因为错误的回环会导致算法出现严重的错误
检测相似性可以采用词袋的做法。
词袋(Bag-of-Words BoW),目的是用“图像上有哪几种特征”来描述一个图像
由于度量的是“是否存在”,所以比通过灰度判断更加稳定
由于度量的不是“在哪里存在”,对空间位置和排序无关,所以对微小运动不敏感
词袋中会有各种概念,对应到不同单词上,而所有单词组成了字典
直观上理解,这些概念可以是“人,车,狗”等等具象的概念
比如一张图像中有两个人和一辆车,我们就可以用向量[ 2 , 1 , 0 ] T [2,1,0]^T [ 2 , 1 , 0 ] T
但实际上常常是采用较为抽象的概念,例如“概念1,概念2,概念3”
这张图像对于这些概念的出现情况也可以写成一个向量
而这些概念集合,对应到单词集合,组成了字典
回想一下词袋模型,可以概括为一个图像中的特征可以分为几个概念,每个概念的数量是多少
而在图像集中分出这些概念,也就是获取字典的过程,实质上是个聚类的过程,可以用经典的Kmeans解决
对于图像,我们可以将提取的特征点(通过其描述子)聚类成一个含有多个单词的字典
但是这种方式的查找效率不高,常采用k k k
假设对于N N N d d d k k k
1.在根节点把所有样本聚成k类
2.对于每一层的每个节点,把属于该节点的样本再聚成k类
3.以此类推,最后获得叶子层,也就是Words
这样子这个树可以容纳k d k^d k d
有了字典,我们就可以通过字典中的单词来表示图像,进而计算相似度
对于特定特征f i f_i f i w j w_j w j
当查找完所有之后,我们可以获得在字典(所有单词)中,这幅图像所对应的单词分布
上述操作是默认每个词同样重要,但是实际上每个词的重要程度是不一样的
常用的方法是TF-IDF(Term Frequency-Inverse Document Frequency),即译频率-逆文档频率
TF 的思想是,某单词在一个图像中经常出现,它的区分度就高。
IDF 的思想是,某单词在字典中出现的频率越低,则分类图像时区分度越高
对于TF:假设图像中单词w i w_i w i m i m_i m i m m m T F i = m i m TF_i=\frac{m_i}{m} T F i = m m i
对于IDF:假设有n n n w i w_i w i n i n_i n i I D F i = l o g n n i IDF_i=log\frac{n}{n_i} I D F i = l o g n i n
于是单词的权重η i = T F i × I D F i \eta_i=TF_i \times IDF_i η i = T F i × I D F i
所以对于一个图像,它的特征点可对应到多个单词,组成它的BoW,用w w w η \eta η
A = ( w 1 , η 1 ) , ( w 2 , η 2 ) , . . . , ( w N , η N ) ≜ v A A={(w_1,\eta_1),(w_2,\eta_2),...,(w_N,\eta_N)} \triangleq v_A A = ( w 1 , η 1 ) , ( w 2 , η 2 ) , . . . , ( w N , η N ) ≜ v A
若采用L1范数,相似度公式表示为:s ( v A , v B ) = 2 ∑ i ( ∣ v A i ∣ + ∣ v B i ∣ − ∣ v A i − v B i ∣ ) s(v_A,v_B)=2\sum_{i}(\vert v_{Ai}\vert+\vert v_{Bi}\vert-\vert v_{Ai} - v_{Bi}\vert) s ( v A , v B ) = 2 ∑ i ( ∣ v A i ∣ + ∣ v B i ∣ − ∣ v A i − v B i ∣ )
之前接触的的特征点地图,是局部地图,用于定位
但如果有导航,避障,重建等需求,就需要稠密地图
进一步地,如果有交互的需求,可能还需要语义地图
稠密深度图估计中,我们不能把每个像素都当做特征点,计算描述子
为了匹配不同图中的像素,我们要用到极线搜索和块匹配
在一个视角中,像素p 1 p_1 p 1
在另一个视角中,这条射线的投影形成图像平面上的一条线,这条投影线就是极线
当我们知道两个视角之间的运动时,极线也就可以确定了
所以要找p 1 p_1 p 1
由于单纯靠单个像素的灰度做匹配十分不稳定,所以采用块匹配技术
在p 1 p_1 p 1
假设取p 1 p_1 p 1 w × w w \times w w × w A A A n n n B B B
我们需要取差值最小的块,存在若干种计算方法(i = 1 , 2 , . . . , w , j = 1 , 2 , . . . , w i=1,2,...,w,\,\,\,j=1,2,...,w i = 1 , 2 , . . . , w , j = 1 , 2 , . . . , w
1.SAD(Sum of Absolute Distance),绝对距离之和,S ( A , B ) S A D = ∑ i , j ∣ A ( i , j ) − B ( i , j ) ∣ S(A,B)_{SAD}=\sum_{i,j} \vert A(i,j) - B(i,j)\vert S ( A , B ) S A D = ∑ i , j ∣ A ( i , j ) − B ( i , j ) ∣
2.SSD(Sum of Squared Distance),平方距离之和,S ( A , B ) S S D = ∑ i , j ( A ( i , j ) − B ( i , j ) ) 2 S(A,B)_{SSD}=\sum_{i,j} ( A(i,j) - B(i,j))^2 S ( A , B ) S S D = ∑ i , j ( A ( i , j ) − B ( i , j ) ) 2
3.NCC(Normalized Cross Correlation),归一化相关性,S ( A , B ) N C C = ∑ i , j A ( i , j ) B ( i , j ) ∑ i , j A ( i , j ) 2 ∑ i , j B ( i , j ) 2 S(A,B)_{NCC}=\frac{\sum_{i,j}A(i,j)B(i,j)}{\sqrt{\sum_{i,j}A(i,j)^2\sum_{i,j}B(i,j)^2}} S ( A , B ) N C C = ∑ i , j A ( i , j ) 2 ∑ i , j B ( i , j ) 2 ∑ i , j A ( i , j ) B ( i , j )
4.上述方法去均值,允许整体亮度有一个差值
通过上述方法,可以找到匹配的两个点p 1 , p 2 p_1,p_2 p 1 , p 2 ( u 1 , v 1 ) (u_1,v_1) ( u 1 , v 1 ) ( u 2 , v 2 ) (u_2,v_2) ( u 2 , v 2 )
接下来我们要计算他的深度,假设深度分别是d 1 d_1 d 1 d 2 d_2 d 2
得归一化向量f 1 = 1 n 1 [ u 1 − c x f x v 1 − c y f y 1 ] , f 2 = 1 n 2 [ u 2 − c x f x v 2 − c y f y 1 ] f_1 = \frac{1}{n_1}\begin{bmatrix} \frac{u_1-c_x}{f_x} \\ \frac{v_1-c_y}{f_y} \\ 1\end{bmatrix},f_2=\frac{1}{n_2}\begin{bmatrix} \frac{u_2-c_x}{f_x} \\ \frac{v_2-c_y}{f_y} \\ 1\end{bmatrix} f 1 = n 1 1 ⎣ ⎢ ⎡ f x u 1 − c x f y v 1 − c y 1 ⎦ ⎥ ⎤ , f 2 = n 2 1 ⎣ ⎢ ⎡ f x u 2 − c x f y v 2 − c y 1 ⎦ ⎥ ⎤
因为P 1 = R P 2 + t P_1 = RP_2 +t P 1 = R P 2 + t
则有d 1 f 1 = d 2 R f 2 + t d_1 f_1 = d_2 R f_2 + t d 1 f 1 = d 2 R f 2 + t
则[ f 1 T f 1 − f 1 T R f 2 f 2 T f 1 − f 2 T R f 2 ] [ d 1 d 2 ] = [ f 1 T t f 2 T t ] \begin{bmatrix} f_1^Tf_1 & -f_1^TRf_2 \\ f_2^Tf_1 & -f_2^TRf_2\end{bmatrix} \begin{bmatrix} d_1 \\ d_2 \end{bmatrix} = \begin{bmatrix} f_1^Tt \\ f_2^Tt \end{bmatrix} [ f 1 T f 1 f 2 T f 1 − f 1 T R f 2 − f 2 T R f 2 ] [ d 1 d 2 ] = [ f 1 T t f 2 T t ]
则[ a 1 a 2 a 3 a 4 ] [ d 1 d 2 ] = [ b 1 b 2 ] \begin{bmatrix} a_1 & a_2 \\ a_3 & a_4\end{bmatrix} \begin{bmatrix} d_1 \\ d_2 \end{bmatrix} = \begin{bmatrix} b_1 \\ b_2 \end{bmatrix} [ a 1 a 3 a 2 a 4 ] [ d 1 d 2 ] = [ b 1 b 2 ]
[ d 1 d 2 ] = 1 a 1 a 4 − a 2 a 3 [ a 4 − a 2 − a 3 a 1 ] [ b 1 b 2 ] \begin{bmatrix} d_1 \\ d_2 \end{bmatrix} = \frac{1}{a_1a_4-a_2a_3}\begin{bmatrix} a_4 & -a_2 \\ -a_3 & a_1\end{bmatrix}\begin{bmatrix} b_1 \\ b_2 \end{bmatrix} [ d 1 d 2 ] = a 1 a 4 − a 2 a 3 1 [ a 4 − a 3 − a 2 a 1 ] [ b 1 b 2 ]
取均值f = d 1 f 1 + d 2 R f 2 + t 2 f= \frac{d_1f_1+d_2Rf_2+t}{2} f = 2 d 1 f 1 + d 2 R f 2 + t f f f
通过上述计算,一个A A A n n n B B B
通常情况下,这个分布存在着许多峰值,我们可以取最大的峰值对应的像素点来计算深度
在多帧的情况下,某些错误的峰值可能达到最大,进而导致误匹配,导致计算的深度错误
所以对于估计的深度,往往是采用一个概率分布来描述
假设深度d d d P ( d ) = N ( μ , σ 2 ) P(d)=N(\mu,\sigma^2) P ( d ) = N ( μ , σ 2 )
假设新计算的深度P ( d n o w ) = N ( μ n o w , σ n o w 2 ) P(d_{now})=N(\mu_{now},\sigma_{now}^2) P ( d n o w ) = N ( μ n o w , σ n o w 2 )
高斯融合后的结果会更可靠,P ( d f u s e ) = N ( σ n o w 2 μ + σ 2 μ n o w σ 2 + σ n o w 2 , σ 2 σ n o w 2 σ 2 + σ n o w 2 ) P(d_{fuse})=N(\frac{\sigma_{now}^2\mu+\sigma^2\mu_{now}}{\sigma^2+\sigma_{now}^2},\frac{\sigma^2\sigma_{now}^2}{\sigma^2+\sigma_{now}^2}) P ( d f u s e ) = N ( σ 2 + σ n o w 2 σ n o w 2 μ + σ 2 μ n o w , σ 2 + σ n o w 2 σ 2 σ n o w 2 )
μ n o w \mu_{now} μ n o w σ n o w 2 \sigma_{now}^2 σ n o w 2
假设只考虑由几何关系带来的不确定性
对于下图,O 1 P O_1 P O 1 P p p p O 1 O 2 O_1O_2 O 1 O 2 t t t
则O 2 P O_2P O 2 P a = p − t a=p-t a = p − t
则α = a r c c o s ⟨ p , t ⟩ , β = a r c o s ⟨ a , − t ⟩ \alpha = arccos\langle p,t\rangle \, , \, \beta=arcos\langle a,-t\rangle α = a r c c o s ⟨ p , t ⟩ , β = a r c o s ⟨ a , − t ⟩
对于向量m 1 , m 2 m_1,m_2 m 1 , m 2 c o s θ = m 1 ⋅ m 2 ∣ m 1 ∣ ∣ m 2 ∣ cos\theta = \frac{m_1 \cdot m_2}{ \vert m_1\vert \vert m_2\vert} c o s θ = ∣ m 1 ∣ ∣ m 2 ∣ m 1 ⋅ m 2
对于p 2 p_2 p 2 β \beta β δ β = a r c t a n 1 f \delta\beta=arctan\frac{1}{f} δ β = a r c t a n f 1
正弦定理有∣ ∣ p ′ ∣ ∣ ∣ ∣ t ∣ ∣ = s i n β ′ s i n ( π − α − β ′ ) = s i n ( β − δ β ) s i n ( π − α − β + δ β ) \frac{\vert\vert p'\vert\vert}{\vert\vert t\vert\vert}=\frac{sin\beta'}{sin(\pi-\alpha-\beta')}=\frac{sin(\beta-\delta\beta)}{sin(\pi-\alpha-\beta+\delta\beta)} ∣ ∣ t ∣ ∣ ∣ ∣ p ′ ∣ ∣ = s i n ( π − α − β ′ ) s i n β ′ = s i n ( π − α − β + δ β ) s i n ( β − δ β )
故单个像素的不确定引起的深度不确定性σ n o w = ∣ ∣ p ∣ ∣ − ∣ ∣ p ′ ∣ ∣ \sigma_{now} = \vert\vert p\vert\vert-\vert\vert p'\vert\vert σ n o w = ∣ ∣ p ∣ ∣ − ∣ ∣ p ′ ∣ ∣
深度估计过程可以概括为:
1.假设所有像素满足高斯分布
2.极线搜索找到对应的像素点
3.三角化计算深度和不确定性
4.融合上一次的数据直到收敛
下载数据集: http://rpg.ifi.uzh.ch/datasets/remode_test_data.zip
①图像块没有区分度(没有纹理),会导致误匹配
②当像素梯度与极线夹角较小时,极线匹配的不确定性大;夹角较大时,极线匹配的不确定性小。
③深度其实不是很满足高斯分布,现在常常用深度的倒数-逆深度,将逆深度近似为高斯分布更为有效
④如果相机旋转,会导致同一个图像块的相关性为负,所以在块匹配之前,通常要通过仿射变换矩阵,将像素变换后再匹配。
RGBD相机获得深度简单且可靠,建图也容易
点云地图是较为基础的,简单来讲就是每一个点的XYZ,它更接近于传感器读取的原始数据。
点云地图存在几个问题
①规模太大了,且提供了很多不必要的细节。
②点云地图无法处理运动物体,只有“添加点”,而没有“当点消失时把它移除”
所以有了八叉树地图
把三维空间建模为许多个小方块,每一个小方块可以分成八个小方块,这八个小方块又分别能分成八个小方块,以此类推…
那么,整个从最大空间细分到最小空间的过程,就是一棵八叉树
但是从上述表述中还没法体现看出八叉树地图有什么优势
因为点云地图同样可以做到,只需要用体素滤波限制体素大小和八叉树叶子节点一样大小即可
对于八叉树地图,在节点中会存储它是否被占据的信息
当某个方块的所有子节点都被占据或都不被占据时,就没必要展开这个节点
例如地图为空白时,我们就只需一个根节点,而不需要完整的树
实际的物体经常连在一起,空白的地方也常常会连在一起,所以大多数八叉树节点都无需展开到叶子层面。
所以说,八叉树比点云节省了大量的存储空间
而且有被占据的信息,相当于我们建模了地图中的障碍物信息
节点中存储它是否被占据的信息,这个信息一般我们用概率表示,假设为x x x
然后我们引入一个新的变量y y y y y y
然后用概率对数值 将y y y [ 0 , 1 ] [0,1] [ 0 , 1 ] x x x x = l o g i t − 1 ( y ) = e x p ( y ) e x p ( y ) + 1 x = logit^{-1}(y)=\frac{exp(y)}{exp(y)+1} x = l o g i t − 1 ( y ) = e x p ( y ) + 1 e x p ( y )
刚开始y y y x x x y y y x x x y y y x x x
所以我们就可以用RGB-D数据,更新八叉树地图了
假设我们观测到某个像素带有深度d,说明这个深度值对应的空间点上观察到了一个占据数据
并且,从相机光心出发,到这个点的线段上,是没有物体的
官方链接:https://github.com/OctoMap/octomap
看README,好像没有说依赖doxygen,我就没装
要同时编译octomap和octovis,只需要对整个进行编译就好了
git clone https://github.com/OctoMap/octomap.git
cd octomap
mkdir build && cd build
cmake ..
make
sudo make install
MonoSLAM:第一个实时的单目视觉SLAM系统,是通过EKF实现的
PTAM:视觉SLAM首次区分前后端,首次用非线性优化取代EKF,引入关键帧机制,同时是一个增强现实软件
ORB-SLAM:是现代主流的特征点 SLAM 的一个高峰,支持单目,双目,RGBD,回环是亮点
LSD-SLAM:单目直接法,半稠密地图,CPU实时
SVO:稀疏直接法,速度非常快,提出了深度滤波器的概念
RTAB-MAP:RGBD SLAM的一个经典方案
两个大方向:视觉惯导融合和语义SLAM、
其他一些方向:基于线/面特征的SLAM、动态场景下的SLAM、多机器人的 SLAM
完结撒花!!!